题目内容
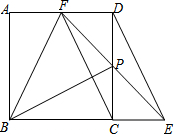 如图,在正方形ABCD中,点P是CD边上的点,连结BP,将△BCP绕点C按顺时针方向旋转90°,得到△DCE,连结EP并延长,交AD于点F,连结BF、FC.
如图,在正方形ABCD中,点P是CD边上的点,连结BP,将△BCP绕点C按顺时针方向旋转90°,得到△DCE,连结EP并延长,交AD于点F,连结BF、FC.(1)证明△CEP是等腰直角三角形;
(2)若CD=2CP,证明:四边形CEDF是平行四边形;
(3)若CD=kCP(k是常数,k>0),记△BPF的面积为s1,△DEP的面积为s2,证明:s1=(k+1)s2.
考点:正方形的性质,全等三角形的判定与性质,等腰直角三角形,平行四边形的判定与性质
专题:
分析:(1)根据旋转的性质可得CE=CP,∠ECP=90°,然后根据等腰直角三角形的定义判定即可;
(2)求出CP=PD,再利用“角边角”证明△CPE和△DPF全等,根据全等三角形对应边相等可得CE=DF,然后根据一组对边平行且相等的四边形是平行四边形证明即可;
(3)设CP=1,表示出CD=k,然后根据S1=S△BEF-S△BEP利用三角形的面积公式列式整理,再表示出S2,然后相比即可得解.
(2)求出CP=PD,再利用“角边角”证明△CPE和△DPF全等,根据全等三角形对应边相等可得CE=DF,然后根据一组对边平行且相等的四边形是平行四边形证明即可;
(3)设CP=1,表示出CD=k,然后根据S1=S△BEF-S△BEP利用三角形的面积公式列式整理,再表示出S2,然后相比即可得解.
解答:解:(1)由于旋转的性质可知,CE=CP,∠ECP=90°,
∵△CEP是等腰直角三角形;
(2)∵CD=2CP,
∴CP=PD,
∵四边形ABCD是正方形,AD∥BC,
∴∠FDP=∠ECP=90°,
在△CPE和△DPF中,
,
∴△CPE≌△DPF(ASA),
∴CE=DF,
又∵CE∥DF,
∴四边形CEDF是平行四边形;
(3)∵CD=kCP,
∴设CP=CE=1,则CD=k,
S1=S△BEF-S△BEP,
=
(k+1)•k-
(k+1)•1,
=
(k+1)(k-1),
S2=
DP•CE=
(k-1)•1,
∵
=
=k+1,
∴s1=(k+1)s2.
∵△CEP是等腰直角三角形;
(2)∵CD=2CP,
∴CP=PD,
∵四边形ABCD是正方形,AD∥BC,
∴∠FDP=∠ECP=90°,
在△CPE和△DPF中,
|
∴△CPE≌△DPF(ASA),
∴CE=DF,
又∵CE∥DF,
∴四边形CEDF是平行四边形;
(3)∵CD=kCP,
∴设CP=CE=1,则CD=k,
S1=S△BEF-S△BEP,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
∵
| S1 |
| S2 |
| ||
|
∴s1=(k+1)s2.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定,平行四边形的判定,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
4的算术平方根是( )
| A、2 |
| B、-2 |
| C、±2 |
| D、a2+a2=a4 |
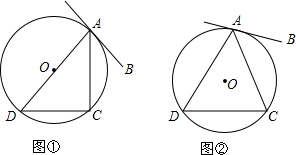 如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求:
如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求: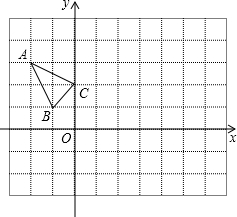 △ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).