题目内容
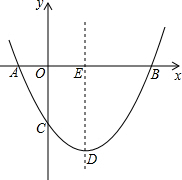 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:轴对称-最短路线问题,二次函数的性质
专题:
分析:把点A的坐标代入抛物线解析式求出b的值,然后求出点C、D的坐标,再求出点C关于x轴的对称点C′的坐标,利用待定系数法求函数解析式直线C′D的解析式,然后令y=0求解即可.
解答:解:∵抛物线y=
x2+bx-2经过点A(-1,0),
∴
×(-1)2+b×(-1)-2=0,
解得b=-
,
∴函数解析式为y=
x2-
x-2,
∵y=
x2-
x-2=
(x-
)2-2-
,
=
(x-
)2-
,
∴顶点D的坐标为(
,-
),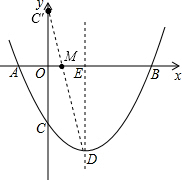
令x=0,则y=-2,
∴点C的坐标为(0,-2),
∴点C关于x轴的对称点C′的坐标为(0,2),
连接C′D与x轴的交点即为所求的MC+MD的值最小时的点M,
设直线C′D的解析式为y=kx+b,
则
,
解得
,
∴直线C′D的解析式为y=-
x+2,
令y=0,则-
x+2=0,
解得x=
,
∴m=
.
故选:B.
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得b=-
| 3 |
| 2 |
∴函数解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
∵y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴顶点D的坐标为(
| 3 |
| 2 |
| 25 |
| 8 |

令x=0,则y=-2,
∴点C的坐标为(0,-2),
∴点C关于x轴的对称点C′的坐标为(0,2),
连接C′D与x轴的交点即为所求的MC+MD的值最小时的点M,
设直线C′D的解析式为y=kx+b,
则
|
解得
|
∴直线C′D的解析式为y=-
| 41 |
| 12 |
令y=0,则-
| 41 |
| 12 |
解得x=
| 24 |
| 41 |
∴m=
| 24 |
| 41 |
故选:B.
点评:本题考查了轴对称确定最短路线问题,二次函数的性质,待定系数法求二次函数解析式,待定系数法求一次函数解析式,确定出点M的位置并求出点C′、D的坐标是解题的关键.

练习册系列答案
相关题目
4的算术平方根是( )
| A、2 |
| B、-2 |
| C、±2 |
| D、a2+a2=a4 |
 实数a、b、c,如图,化简
实数a、b、c,如图,化简 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是
如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是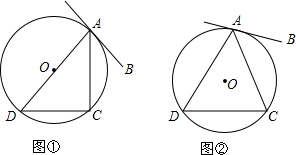 如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求:
如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求: