题目内容
 如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=
如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=| 2 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:根据反比例函数系数k的几何意义可得S△DBO=S△AOC=
|k|=1,再利用矩形OCPD的面积减去△BDO和△CAO的面积即可.
| 1 |
| 2 |
解答:4解:∵B、A两点在反比例函数y=
(x>0)的图象上,
∴S△DBO=S△AOC=
×2=1,
∵P(2,3),
∴四边形DPCO的面积为2×3=6,
∴四边形BOAP的面积为6-1-1=4,
故答案为4.
| 2 |
| x |
∴S△DBO=S△AOC=
| 1 |
| 2 |
∵P(2,3),
∴四边形DPCO的面积为2×3=6,
∴四边形BOAP的面积为6-1-1=4,
故答案为4.
点评:此题主要考查了反比例函数k的几何意义,关键是掌握在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
|k|,且保持不变.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
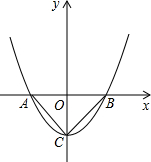 如图,抛物线y=x2+m与x轴交于点C,若∠ACB=90°,求抛物线的解析式.
如图,抛物线y=x2+m与x轴交于点C,若∠ACB=90°,求抛物线的解析式. 如图,在△ABC中,CD⊥AE,∠BAE=25°,∠BCD=20°,则∠B=
如图,在△ABC中,CD⊥AE,∠BAE=25°,∠BCD=20°,则∠B= 如图,抛物线y=ax2-4ax+m与x轴交A(1,0),B(x2,0),则x1=
如图,抛物线y=ax2-4ax+m与x轴交A(1,0),B(x2,0),则x1= 已知,AB是⊙O的直径,弦CD⊥AB,E是
已知,AB是⊙O的直径,弦CD⊥AB,E是