题目内容
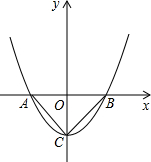 如图,抛物线y=x2+m与x轴交于点C,若∠ACB=90°,求抛物线的解析式.
如图,抛物线y=x2+m与x轴交于点C,若∠ACB=90°,求抛物线的解析式.考点:抛物线与x轴的交点
专题:
分析:直接利用等腰直角三角形的性质以及抛物线的性质得出AO=BO=CO=|m|,进而得出m的值即可.
解答:解:∵抛物线y=x2+m其对称轴为y轴,∠ACB=90°,
∴△ACB是等腰直角三角形,
∴AO=BO=CO=|m|,
∴A(m,0),
故0=m2+m,
解得:m1=0(不合题意舍去),m2=-1.
故抛物线的解析式为:y=x2-1.
∴△ACB是等腰直角三角形,
∴AO=BO=CO=|m|,
∴A(m,0),
故0=m2+m,
解得:m1=0(不合题意舍去),m2=-1.
故抛物线的解析式为:y=x2-1.
点评:此题主要考查了抛物线与x轴的交点问题和等腰直角三角形的性质,得出AO=BO=CO=|m|是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:AB∥CD,AD∥BC.求证:OA=OC,OB=OD.
已知:AB∥CD,AD∥BC.求证:OA=OC,OB=OD.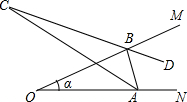 如图,已知∠MON=α,点A、B分别在射线ON、OM上移动(不与点O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若改变,说明理由;若不改变,求出其值.
如图,已知∠MON=α,点A、B分别在射线ON、OM上移动(不与点O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若改变,说明理由;若不改变,求出其值. 如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=
如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y= 如图,直线a∥b,矩形ABCD的顶点B在直线b上,则∠α的度数是
如图,直线a∥b,矩形ABCD的顶点B在直线b上,则∠α的度数是