题目内容
18.如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2017的坐标为(4033,1).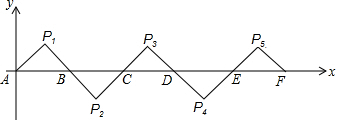
分析 作P1⊥x轴于H,利用等腰直角三角形的性质得P1H=$\frac{1}{2}$AB=1,AH=BH=1,则P1的纵坐标为1,再利用旋转的性质易得P2的纵坐标为-1,P3的纵坐标为1,P4的纵坐标为-1,P5的纵坐标为1,…,于是可判断P1017的纵坐标为1,而横坐标为2017×2-1=4033,所以P1017(4033,1).
解答 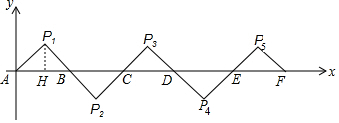 解:作P1⊥x轴于H,
解:作P1⊥x轴于H,
∵A(0,0),B(2,0),
∴AB=2,
∵△AP1B是等腰直角三角形,
∴P1H=$\frac{1}{2}$AB=1,AH=BH=1,
∴P1的纵坐标为1,
∵△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,
∴P2的纵坐标为-1,P3的纵坐标为1,P4的纵坐标为-1,P5的纵坐标为1,…,
∴P1017的纵坐标为1,横坐标为2017×2-1=4033,
即P1017(4033,1).
故答案为:(4033,1).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | a(a-1)=a2-a | B. | (a4)3=a7 | C. | a4+a3=a7 | D. | 2a5÷a3=a2 |
15.下面几何体的主视图为( )


| A. |  | B. |  | C. |  | D. |  |
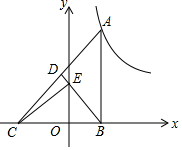 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.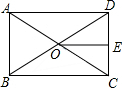 如图,在矩形ABCD中,AC、BD相交于点O,OE⊥CD.求证:OE=$\frac{1}{2}$AD.
如图,在矩形ABCD中,AC、BD相交于点O,OE⊥CD.求证:OE=$\frac{1}{2}$AD. 如图,EB∥DC,∠C=∠E,∠A和∠ADE有何关系?并说明你的理由.
如图,EB∥DC,∠C=∠E,∠A和∠ADE有何关系?并说明你的理由.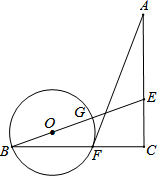 如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F.
如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F.