题目内容
13.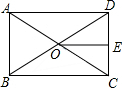 如图,在矩形ABCD中,AC、BD相交于点O,OE⊥CD.求证:OE=$\frac{1}{2}$AD.
如图,在矩形ABCD中,AC、BD相交于点O,OE⊥CD.求证:OE=$\frac{1}{2}$AD.
分析 由矩形ABCD中对角线AC、BD相交于点O,OE⊥CD,易得OE是△DBC的中位线,继而求得答案.
解答 证明:∵四边形ABCD是正方形,
∴OB=OD,∠BCD=90°,
∵OE⊥CD,
∴∠OED=90°,
∴OE∥BC,
∴OE是△DBC的中位线,
∴OE=$\frac{1}{2}$BC,
∴OE=$\frac{1}{2}$AD.
点评 此题考查了矩形的性质以及三角形中位线的性质.注意证得OE是△DBC的中位线是关键.

练习册系列答案
相关题目
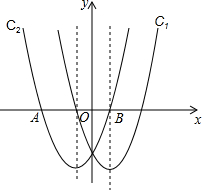 在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.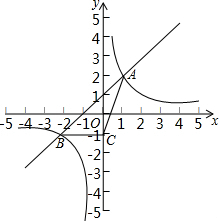 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.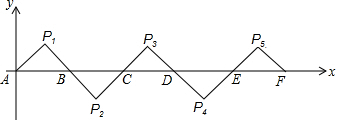
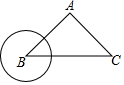 如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.
如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$. 如图,在菱形ABCD中,∠BAD=135°,AB=4$\sqrt{2}$,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为8$\sqrt{2}$-8.
如图,在菱形ABCD中,∠BAD=135°,AB=4$\sqrt{2}$,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为8$\sqrt{2}$-8.