题目内容
当代数式
+
+
取得最小值时,x+y= .
| x2+6x+13 |
| x2+y2 |
| y2-4y+5 |
考点:无理函数的最值
专题:数形结合
分析:可将不熟悉的“求三个二次根式和的最小值”的问题转化为熟悉的“求三条线段和的最小值“的问题.若A的坐标为(-3,2),B的坐标为(x,0),C的坐标为(0,y),D的坐标为(1,2),则根据勾股定理可得AB=
,BC=
,CD=
,从而得到原式=AB+BC+CD,只需求出AB+BC+CD的最小值就可解决问题.
| x2+6x+13 |
| x2+y2 |
| y2-4y+5 |
解答:解:如图,A的坐标为(-3,2),D的坐标为(1,2),点B在x轴上,点C在y轴上,
过点A作AE⊥x轴于E,过点D作DF⊥x轴于F,延长DF到点D′,使得FD′=FD,
连接AD交y轴于点H,连接AB、BC、CD、BD、BD′、AD′,
则DH⊥y轴,AD⊥DD′,BD=BD′,点D′的坐标为(1,-2).
设B的坐标为(x,0),C的坐标为(0,y),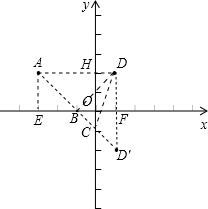
在Rt△AEB中,
∵AE=2,BE=
=
,
∴AB=
=
=
.
在Rt△BOC中,
∵OB=
,OC=
,
∴BC=
=
.
在Rt△DHC中,
∵DH=1,CH=
,
∴CD=
=
=
.
∴原式=AB+BC+CD.
根据两点之间线段最短可得:
当B、C、D三点共线时,BC+CD最短,等于BD长
此时AB+BC+CD的最小值等于AB+BD.
∵BD=BD′,∴AB+BD=AB+BD′.
根据两点之间线段最短可得:
当A、B、D′三点共线时,AB+BD′最短,等于AD′长.
设直线AD′的解析式为y=kx+b,
则
.
解得:
.
∴直线AD′的解析式为y=-x-1.
当x=0时,y=-1;当y=0时,x=-1.
∴当代数式
+
+
取得最小值时,x=-1,y=-1.
∴x+y=-2.
故答案为:-2.
过点A作AE⊥x轴于E,过点D作DF⊥x轴于F,延长DF到点D′,使得FD′=FD,
连接AD交y轴于点H,连接AB、BC、CD、BD、BD′、AD′,
则DH⊥y轴,AD⊥DD′,BD=BD′,点D′的坐标为(1,-2).
设B的坐标为(x,0),C的坐标为(0,y),

在Rt△AEB中,
∵AE=2,BE=
|
|
∴AB=
| AE2+BE2 |
| 22+(x+3)2 |
| x2+6x+13 |
在Rt△BOC中,
∵OB=
|
|
∴BC=
| OB2+OC2 |
| x2+y2 |
在Rt△DHC中,
∵DH=1,CH=
|
∴CD=
| DH2+CH2 |
| 12+(y-2)2 |
| y2-4y+5 |
∴原式=AB+BC+CD.
根据两点之间线段最短可得:
当B、C、D三点共线时,BC+CD最短,等于BD长
此时AB+BC+CD的最小值等于AB+BD.
∵BD=BD′,∴AB+BD=AB+BD′.
根据两点之间线段最短可得:
当A、B、D′三点共线时,AB+BD′最短,等于AD′长.
设直线AD′的解析式为y=kx+b,
则
|
解得:
|
∴直线AD′的解析式为y=-x-1.
当x=0时,y=-1;当y=0时,x=-1.
∴当代数式
| x2+6x+13 |
| x2+y2 |
| y2-4y+5 |
∴x+y=-2.
故答案为:-2.
点评:本题主要考查了用待定系数法求一次函数的解析式、线段的垂直平分线的性质、勾股定理、两点之间线段最短等知识,考查了创造性思维和数形结合的思想,而把问题转化为求线段和的最小值是解决本题的关键.

练习册系列答案
相关题目
某市为迎接大学生冬季运动会,正在进行城区人行道路翻新,准备只选用同一种正多边形地砖铺设地面.下列正多边形的地砖中,不能进行平面镶嵌的是( )
| A、正三角形 | B、正方形 |
| C、正六边形 | D、正八边形 |
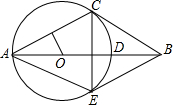 在△ABC中,tanA=
在△ABC中,tanA=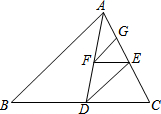 如图,AD是△ABC的中线,E是AC的中点,F是AD的中点,G是AE的中点,若△AFG的面积是2,则△ABC的面积是
如图,AD是△ABC的中线,E是AC的中点,F是AD的中点,G是AE的中点,若△AFG的面积是2,则△ABC的面积是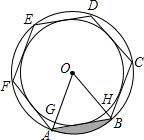 如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.
如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.
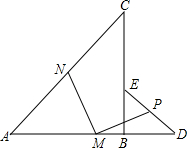 将等腰Rt△ABC和等腰Rt△BDE的直角顶点B重合,M、N、P分别是AD、AC、DE边的中点,且A、B、D在同一直线上,试说明MP与MN的关系.
将等腰Rt△ABC和等腰Rt△BDE的直角顶点B重合,M、N、P分别是AD、AC、DE边的中点,且A、B、D在同一直线上,试说明MP与MN的关系.