题目内容
19．
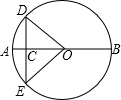如图，C是⊙O的直径AB上一点，过点C作弦DE，使CD=CO，若∠AOD=40°，求$\widehat{BD}$，$\widehat{AE}$的度数．
分析 根据等腰三角形的性质：等边对等角以及三角形的外角等于不相邻的两个内角的和即可求解．
解答 解：∵DC=OC，
∴∠D=∠AOD=40°，
∴∠OCD=180°-∠D-∠AOD=100°，
∴∠BOD=120°，
∴$\widehat{BD}$的度数是120°，
∵OD=OE，
∴∠E=∠D=40°，
∴∠BOE=∠E+∠OCE=40°+80°=120°，
∴∠AOE=60°，
∴$\widehat{AE}$的度数是60°．
点评 本题考查了等腰三角形的性质，以及三角形的外角的性质，理解性质是关键．
练习册系列答案
相关题目
7．已知变量x、y满足下面的关系：
根据表格中y与x之间的变化规律，写出y与x之间的关系式为y=$\frac{6}{x}$．
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y | … | -2 | -3 | -6 | 6 | 3 | 2 | … |
如图，已知OP平分∠AOB，用直尺和圆规作图
11．
南县农民一直保持着冬种油菜的习惯，利用农闲冬种一季油菜．南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计，并绘制了如下统计表与统计图：
请根据以上信息解答下列问题：
（1）种植油菜每亩的种子成本是多少元？
（2）农民冬种油菜每亩获利多少元？
（3）2014年南县全县农民冬种油菜的总获利为多少元？（结果用科学记数法表示）
南县农民一直保持着冬种油菜的习惯，利用农闲冬种一季油菜．南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计，并绘制了如下统计表与统计图：| 每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
| 310元 | 130千克 | 5元/千克 | 500000亩 |
（1）种植油菜每亩的种子成本是多少元？
（2）农民冬种油菜每亩获利多少元？
（3）2014年南县全县农民冬种油菜的总获利为多少元？（结果用科学记数法表示）
将一个圆分成4个扇形，已知扇形AOB、AOD、BOD的圆心角的度数之比为2：3：4，OC为∠BOD的角平分线，求这4个扇形的圆心角度数．