题目内容
8.为丰富学校文化社会,切实提高同学们的身心素质,在春意盎然的三月,重庆巴蜀中学第八届春季运动会即将拉开序幕,大会决定购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元,若购买A种奖品5件和B种奖品3件,共需95元.(1)求A、B两种奖品的单价各是多少元?
(2)学校决定购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,请你利用所学函数知识确定最小购买费用的值.
分析 (1)设A奖品的单价是x元,B奖品的单价是y元,根据条件建立方程组求出其解即可;
(2)设总费用为W,根据总费用=两种奖品的费用之和表示出W与m的关系式,并由条件建立不等式组求出m的取值范围,由一次函数的性质就可以求出结论.
解答 解(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
$\left\{\begin{array}{l}{3x+2y=60①}\\{5x+3y=95②}\end{array}\right.$,
解得:
$\left\{\begin{array}{l}{x=10}\\{y=15}\end{array}\right.$.
答:A奖品的单价是10元,B奖品的单价是15元;
(2)设总费用为W,由题意,得
W=10m+15(100-m)=-5m+1500
∴$\left\{\begin{array}{l}{-5m+1500≤1150}\\{m≤3(100-m)}\end{array}\right.$,
解得:70≤m≤75.
∵m是整数,
∴m=70,71,72,73,74,75.
∵W=-5m+1500,
∴k=-5<0,
∴W随m的增大而减小,
∴m=75时,W最小=1125.
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
点评 本题考查了一次函数的性质的运用,二元一次方程组的运用,一元一次不等式组的运用,解答时求一次函数的解析式是关键.

练习册系列答案
相关题目
16.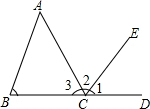 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠2和∠B是同位角 | B. | ∠2和∠B是内错角 | ||
| C. | ∠1和∠A是内错角 | D. | ∠3和∠B是同旁内角 |
3.若x=-1是关于x的一元二次方程ax2+bx-2=0(a≠0)的一个根,则2015-2a+2b的值等于( )
| A. | 2015 | B. | 2011 | C. | 2018 | D. | 2013 |
13.化简$\sqrt{16}$的结果是( )
| A. | ±4 | B. | 4 | C. | 2 | D. | ±2 |
20.若a2=25,|b|=3,则a+b=( )
| A. | 8 | B. | ±8 | C. | ±2 | D. | ±8或±2 |
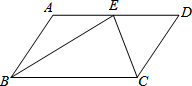 在?ABCD中,∠ABC和∠BCD的平分线交AD边上一点E,且BE=4,CE=3,求AD的长.
在?ABCD中,∠ABC和∠BCD的平分线交AD边上一点E,且BE=4,CE=3,求AD的长.