题目内容
16. 如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 观察图象易得a>0,-$\frac{b}{2a}$=$\frac{1}{3}$>0,所以b<0,因此abc>0,通过变形-$\frac{b}{2a}$=$\frac{1}{3}$进行判断即可.
解答 解:∵抛物线与y轴的交点在x轴下方,
∴c<0,;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=$\frac{1}{3}$,
∴b=-$\frac{2a}{3}$<0,
∴abc>0,所以①错误;
∵x=$\frac{1}{2}$时,y<0,
∴a+2b+4c<0,所以②正确;
∵-$\frac{b}{2a}$=$\frac{1}{3}$,
∴2a+3b=0,所以③正确;
∵x=-1时,y>0得到a-b+c>0,
∴-$\frac{3b}{2}$-b+c>0,于是2c>5b,故④正确.
故选C.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口,当a<0时,抛物线向下;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.抛物线的解析式y=-2(x+3)2+1,则顶点坐标是( )
| A. | (-3,1) | B. | (3,1) | C. | (3,-1) | D. | (1,3) |
8.下列各组算式中,其值最大的是( )
| A. | -32+2 | B. | (-3)2-2 | C. | (-3)2×(-2) | D. | -32÷(-2) |
5.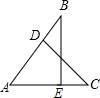 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )| A. | AAS | B. | HL | C. | SSS | D. | SAS |
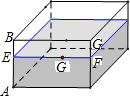 有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).
有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).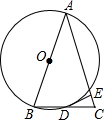 如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.