题目内容
20. 已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.
已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.(1)求m、n的值;
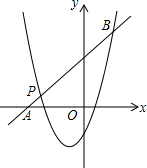
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A(-4,0),与二次函数的图象相交于另一点B,求点B的坐标.
分析 (1)利用抛物线的对称轴方程可求出m的值,然后把P点坐标代入y=x2+2x+n可求出n的值;
(2)先利用待定系数法求出一次函数解析式,然后通过解方程组$\left\{\begin{array}{l}{y={x}^{2}+2x-2}\\{y=x+4}\end{array}\right.$可确定B点坐标.
解答 解:(1)∵对称轴是经过(-1,0)且平行于y轴的直线,
∴抛物线的对称轴为直线x=-1,
即-$\frac{m}{2}$=-1,
∴m=2,
把P(-3,1)代入y=x2+2x+n得9-6+n=1,
∴n=-2;
(2)把P(-3,1),A(-4,0)代入y=kx+b得$\left\{\begin{array}{l}{-3k+b=1}\\{-4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=4}\end{array}\right.$,
所以一次函数解析式为y=x+4,
解方程组$\left\{\begin{array}{l}{y={x}^{2}+2x-2}\\{y=x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$,
所以B点坐标为(2,6).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数与一次函数的交点问题.

练习册系列答案
相关题目
8.下列各组算式中,其值最大的是( )
| A. | -32+2 | B. | (-3)2-2 | C. | (-3)2×(-2) | D. | -32÷(-2) |
5.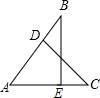 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )| A. | AAS | B. | HL | C. | SSS | D. | SAS |
12.已知下列方程:①xy-1=2;②0.3x=4;③x=1;④x2-4x=3;⑤2x+3y=6,是一元一次方程的有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
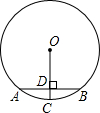 如图,AB为⊙O的弦,OC⊥AB于点D,交⊙O于点C.若⊙O的半径为5,AB=6,则CD的长是1.
如图,AB为⊙O的弦,OC⊥AB于点D,交⊙O于点C.若⊙O的半径为5,AB=6,则CD的长是1.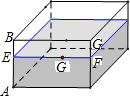 有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).
有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).
 身高为1.8m 的运动员小王进行投篮训练,已知篮圈中心与地面的垂直距离为3.05 m,小王站在与篮圈中心的水平距离4m的地方进行跳投,球的运动路线一条抛物线,当球运行的水平距离为2.5m时,球达到距离地面3.5m的最高点,运行一段时间后篮球最后恰好落入篮圈.
身高为1.8m 的运动员小王进行投篮训练,已知篮圈中心与地面的垂直距离为3.05 m,小王站在与篮圈中心的水平距离4m的地方进行跳投,球的运动路线一条抛物线,当球运行的水平距离为2.5m时,球达到距离地面3.5m的最高点,运行一段时间后篮球最后恰好落入篮圈.