题目内容
15.纳米(记为nm)是一种长度单位.1nm为0.000000001米,请将0.000000001用科学记数法表示为( )| A. | 0.1×10-8 | B. | 1×109 | C. | 0.1×108 | D. | 1×10-9 |
分析 绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解答 解:请将0.000000001用科学记数法表示为1×10-9,
故选:D.
点评 本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.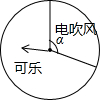 为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
(1)计算上述表格中a、b的值.a=0.71,b=564;
(2)请估计当n很大时,落在“可乐”区域的频率将会接近0.7;假如你去转动该转盘一次,你获得“可乐”的概率约是0.7;(结果全部精确到0.1)
(3)在该转盘中,表示“电吹风”区域的扇形的圆心角a约是多少度?(结果精确到1°)
 为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 72 | 142 | 278 | 355 | b | 701 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.72 | 0.71 | 0.695 | a | 0.705 | 0.701 |
(2)请估计当n很大时,落在“可乐”区域的频率将会接近0.7;假如你去转动该转盘一次,你获得“可乐”的概率约是0.7;(结果全部精确到0.1)
(3)在该转盘中,表示“电吹风”区域的扇形的圆心角a约是多少度?(结果精确到1°)
7.无锡市环保检测中心网站公布的2017年4月某日的PM2.5研究性检测部分数据如表:
则该日这6个时刻的PM2.5的众数和中位数分别是( )
| 时间 | 0:00 | 4:00 | 8:00 | 12:00 | 16:00 | 20:00 |
| PM2.5(mg/m3) | 0.027 | 0.035 | 0.032 | 0.014 | 0.016 | 0.032 |
| A. | 0.032,0.0295 | B. | 0.026,0.0295 | C. | 0.026,0.032 | D. | 0.032,0.027 |
4.已知点A(2,-2),B(-1,-2),则直线AB与x轴的位置关系是( )
| A. | 相交 | B. | 平行 | C. | 相互垂直 | D. | 不能确定 |
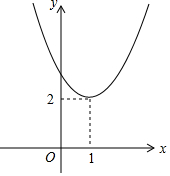 “爱心是人间真情所在”!现用“?”定义一种运算,对任意实数m、n和抛物线y=ax2,当y=ax2?(m,n)后都可得到y=a(x-m)2+n.当y=x2?(m,n)后得到了新函数的图象(如图所示),则nm=2.
“爱心是人间真情所在”!现用“?”定义一种运算,对任意实数m、n和抛物线y=ax2,当y=ax2?(m,n)后都可得到y=a(x-m)2+n.当y=x2?(m,n)后得到了新函数的图象(如图所示),则nm=2. 如图,小丽从A点出发前进6m,向右转40°,再前进6m,又右转40°,…,这样一直走下去,当她第一次回到出发点A时,一共走了54m.
如图,小丽从A点出发前进6m,向右转40°,再前进6m,又右转40°,…,这样一直走下去,当她第一次回到出发点A时,一共走了54m.