题目内容
1.将一些相同的“○”按如图所示的规律,观察每个“稻草人”中的“○”的个数,则第6个“稻草人”中有26个“○”,则第n个“稻草人”中有1+(n+3)+(n-1)2个“○”.
分析 分析数据可得:第1个图形中小圆的个数为1+4=5;第2个图形中小圆的个数为1+5+1=7;第3个图形中小圆的个数为1+6+4=11;第4个图形中小圆的个数为1+7+9=17;…由此得出第n个图形中小圆的个数为1+(n+3)+(n-1)2.据此可以求得答案.
解答 解:∵第1个图形中小圆的个数为1+4=5;
第2个图形中小圆的个数为1+5+1=7;
第3个图形中小圆的个数为1+6+4=11;
第4个图形中小圆的个数为1+7+9=17;
…
∴第n个图形中小圆的个数为1+(n+3)+(n-1)2=n2-n+5
∴第6个“稻草人”中的“○”的个数为62-6+5=35,
故答案为:35,n2-n+5.
点评 此题主要考查了图形的变化规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键,注意公式必须符合所有的图形.

练习册系列答案
相关题目
11. 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )| A. | S1=S2 | B. | S1>S2 | C. | S1<S2 | D. | $S1=\frac{1}{2}S2$ |
6.下列尺规作图,能判断AD是△ABC边上的高是( )
| A. |  | B. |  | C. |  | D. |  |
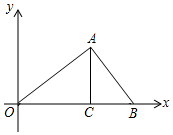 在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.
在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.