题目内容
18. 已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,与y轴交于点C.
已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,与y轴交于点C.(1)求抛物线y=ax2+bx-8(a≠0)的解析式,并求出顶点P的坐标;
(2)求∠APB的正弦值;
(3)直线y=kx+2与y轴交于点N,与直线AC的交点为M,当△MNC与△AOC相似时,求点M的坐标.
分析 (1)根据抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,列出a和b的二元一次方程组,求出a和b的值即可;
(2)设对称轴直线x=1与x轴交于点D,过A作AH⊥BP,垂足为H,先求出AB、PD、AP和BP的长,进而求出AH的长,即可求出sin∠APB的值;
(3)△MNC与△AOC相似时,分①∠MNC=∠AOC=90°和②∠NMC=∠AOC=90°,利用相似三角形的性质以及全等三角形的知识求出点M的坐标.
解答 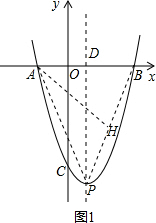 解:(1)∵抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,
解:(1)∵抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,
∴$\left\{\begin{array}{l}{0=4a-2b-8}\\{0=16a+4b-8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴抛物线解析式为y=x2-2x-8,
∵y=x2-2x-8=(x-1)2-9,
∴顶点P坐标为(1,-9);
(2)设对称轴直线x=1与x轴交于点D,过A作AH⊥BP,垂足为H,如图1,
∵A(-2,0),B(4,0),P(1,-9),
∴AB=6,PD=9,AP=BP=3$\sqrt{10}$,
∵$\frac{1}{2}$AB×PD=$\frac{1}{2}$PB×AH,
∴AH=$\frac{9}{5}\sqrt{10}$,
在Rt△APH中,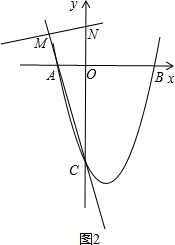
∴sin∠APB=$\frac{AH}{AP}$=$\frac{3}{5}$;
(3)∵∠ACO=∠MCN,
∴△MNC与△AOC相似时,
①∠MNC=∠AOC=90°,
∴$\frac{MN}{AO}=\frac{NC}{OC}$,
∵AO=2,OC=8,NC=10,
∴MN=$\frac{5}{2}$,
直线直线AC的解析式是:y=-4x-8,
设M点坐标为(a,-4a-8),
∵MN=$\frac{5}{2}$,
∴a=-$\frac{5}{2}$,
∴M(-$\frac{5}{2}$,2),
②∠NMC=∠AOC=90°,
设MN与x轴交于点E,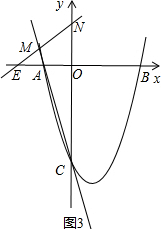
∵$\left\{\begin{array}{l}{ON=OA=2}\\{∠EON=∠AOC=90°}\\{∠NEO=∠ACO}\end{array}\right.$,
∴△ENO≌△AOC(AAS),
∴OE=OC=8,
∴E(-8,0),
∵A(-2,0),C(0,-8)
∴直线MN的解析式是:y=$\frac{1}{4}$x+2,
直线AC的解析式是:y=-4x-8,
联立$\left\{\begin{array}{l}{y=\frac{1}{4}x+2}\\{y=-4x-8}\end{array}\right.$
∴M(-$\frac{40}{17}$,$\frac{24}{17}$),
综上M点的坐标为(-$\frac{5}{2}$,2)或(-$\frac{40}{17}$,$\frac{24}{17}$).
点评 本题主要考查了二次函数综合题的知识,此题涉及到待定系数法求二次函数的解析式、二次函数的性质、相似三角形的判定与性质、全等三角形的判定与性质以及锐角三角形函数值的定义,解答本题的关键是熟练掌握全等三角形的性质以及相似三角形的性质,此题还需要熟练运用分类思想解决问题,此题有一定的难度.

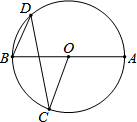 如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )
如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )| A. | 25° | B. | 35° | C. | 55° | D. | 70° |
| A. | y=x+3 | B. | y=x-3 | C. | y=x-1 | D. | y=-x+1 |
 如图,是一个工件的三视图,则此工件的全面积是( )
如图,是一个工件的三视图,则此工件的全面积是( )| A. | 85πcm2 | B. | 90πcm2 | C. | 155πcm2 | D. | 165πcm2 |
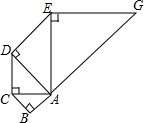 如图,以1为腰长画等腰直角三角形Rt△ACB,又以Rt△ACB的斜边AC长为直角边画第2个等腰直角三角形Rt△ADC,再以Rt△ADC的斜边AD长为直角边画第3个等腰直角三角形Rt△ADE,依此类推,则第2015个等腰直角三角形的斜边长为${(\sqrt{2})}^{2015}$.
如图,以1为腰长画等腰直角三角形Rt△ACB,又以Rt△ACB的斜边AC长为直角边画第2个等腰直角三角形Rt△ADC,再以Rt△ADC的斜边AD长为直角边画第3个等腰直角三角形Rt△ADE,依此类推,则第2015个等腰直角三角形的斜边长为${(\sqrt{2})}^{2015}$.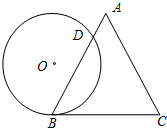 如图,一个边长为8cm的等边△ABC的高与⊙O的直径相等,⊙O与BC相切于点B,⊙O与AB相交于点D,求BD的长.
如图,一个边长为8cm的等边△ABC的高与⊙O的直径相等,⊙O与BC相切于点B,⊙O与AB相交于点D,求BD的长.