题目内容
若直线y=3x+6与直线y=2x+4的交点坐标为(a , b),则解为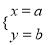 的方程组是( )
的方程组是( )
A. 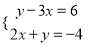 B.
B. 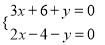 C.
C. 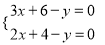 D.
D. 
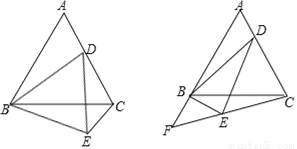
如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;
阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程
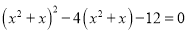
商场某种商品平均每天可销售20件,每件盈利40元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?此时,每件衬衫盈利多少元?
(2)每件衬衫降价多少元,商场平均每天盈利最多?
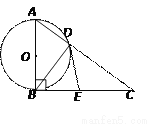
查看答案如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.
某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.
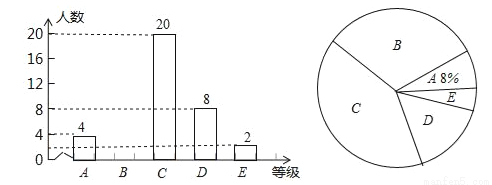
(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
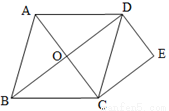
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
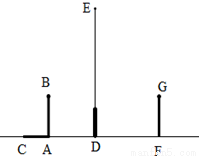
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案在一次朋友聚餐中,有A、B、C、D四种素菜可供选择,小明从中选择一种,小莉也从中选择一种(与小明选择的不相同),请利用列表或树状图的方法求出A与B两种素菜被选中的概率.
查看答案直线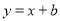 与反比例函数
与反比例函数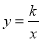 (
(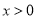 )的图象交于点A(1,2),求这两个函数的表达式.
)的图象交于点A(1,2),求这两个函数的表达式.
解一元二次方程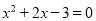
如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
反比例函数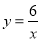 图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A. y2<y1<y3 B. y1<y2<y3 C. y3<y1<y2 D. y3<y2<y1
A 【解析】k=6>0,所以反比例函数图像位于一三象限,并且当x<0时,y随着x的增大而减小,所以y2<y1<y3. 故选A. 点睛:已知反比例函数解析式和点的横坐标要比较纵坐标大小,可以数形结合,借助图像的性质进行比较.一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )
A. 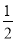 B.
B. 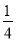 C.
C. 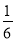 D.
D. 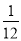
如图,⊙O是△ABC的外接圆,∠OCB=40°则∠A的度数等于( )
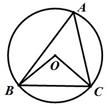
A. 60° B. 50° C. 40° D. 30°
查看答案在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. 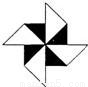 B .
B . C .
C . D.
D. 
已知反比例函数 ,下列结论不正确的是
,下列结论不正确的是
A.图象必经过点(-1,2) B.y随x的增大而增大
C.图象在第二、四象限内D.若x>1,则y>-2
查看答案在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动,设两点移动的时间为t秒,回答下列问题:
(1)如图1,当t为几秒时,△PBQ的面积等于5cm2?
(2)如图2,当t= 秒时,试判断△DPQ的形状,并说明理由;
秒时,试判断△DPQ的形状,并说明理由;
(3)如图3,以Q为圆心,PQ为半径作⊙Q.
①在运动过程中,是否存在这样的t值,使⊙Q正好与四边形DPQC的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由;
②若⊙Q与四边形DPQC有三个公共点,请直接写出t的取值范围.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一次函数y=(m2﹣4)x+(1﹣m)和y=(m﹣1)x+m2﹣3的图象与y轴分别交于点P和点Q,若点P与点Q关于x轴对称,则m=________
-1 【解析】试题解析::∵y=(m2-4)x+(1-m)和y=(m-1)x+m2-3的图象与y轴分别交于点P和点Q, ∴P(0,1-m),Q(0,m2-3) 又∵P点和Q点关于x轴对称 ∴可得:1-m=-(m2-3) 解得:m=2或m=-1. ∵y=(m2-4)x+(1-m)是一次函数, ∴m2-4≠0, ∴m≠±2, ∴m=-1.如图,在△ABC中,∠BAC=90°,AB=AC,∠BAD=30°,AD=AE,则∠EDC的度数是______.
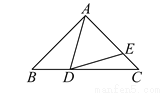
如图,△ABC≌△DEF,A与D,B与E分别是对应顶点,∠B=60°,∠A=68°,AB=13cm,则∠F= ______度,DE= ____cm.
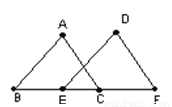
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )
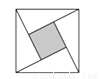
A. 1:2 B. 1:4 C. 1:5 D. 1:10
查看答案如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,若BC=18,DE=8,则△BCE的面积等于( )
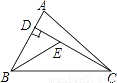
A. 36 B. 54 C. 63 D. 72
查看答案如图,在△ABC中,∠B=∠C,AD为△ABC的中线,那么下列结论错误的是( )
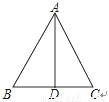
A. △ABD≌△ACD B. AD为△ABC的高线 C. AD为△ABC的角平分线 D. △ABC是等边三角形
查看答案 试题属性- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
用a、b、c作三角形的三边,其中不能构成直角三角形的是( )
A. a2=(b+c)(b﹣c) B. a:b:c=1: 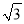 :2
:2
C. a=32,b=42,c=52 D. a=5,b=12,c=13
C 【解析】试题解析:∵a2=(b+c)(b﹣c), ∴a2=b2﹣c2 , ∴a2+c2=b2 , 根据勾股定理的逆定理可得,用a、b、c作三角形的三边,能构成直角三角形,故选项A错误; ∵a:b:c=1: :2, ∴设a=x,b=x,c=2x, ∵, ∴用a、b、c作三角形的三边,能构成直角三角形,故选项B错误; ∵a=32, b=42, ...如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
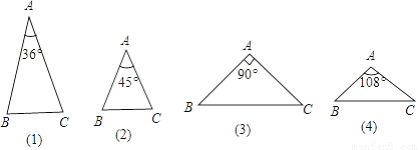
A. (1)(2)(3) B. (1)(3)(4) C. (2)(3)(4) D. (1)(2)(4)
查看答案如图,PB⊥AB于B,PC⊥AC于C,且PB=PC,则△APB≌△APC的理由是( )
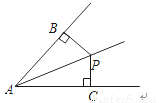
A. SAS B. ASA C. HL D. AAS
查看答案如图,在△ABC中,AB=AC=5,P是BC边上除B,C点外的任意一点,则代数式AP2+PB·PC等于 ( )
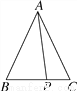
A. 25 B. 15 C. 20 D. 30
查看答案如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
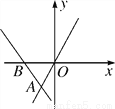
A. x<-2 B. -2<x<-1 C. -2<x<0 D. -1<x<0
查看答案若直线y=3x+6与直线y=2x+4的交点坐标为(a , b),则解为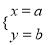 的方程组是( )
的方程组是( )
A. 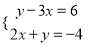 B.
B. 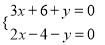 C.
C. 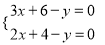 D.
D. 
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.

(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
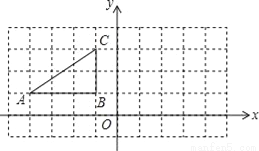
(1)50,144;(2). 【解析】试题分析:(1)用A等级的人数除以A等级所占的百分比求出总人数,再用360°乘以C等级所占的百分比求出C等级所对应扇形的圆心角的度数,再用总人数减去A、C、D、E等级的人数,求出B等级的人数,从而补全统计图; (2)根据题意先列表,得出所有等可能的情况数,找出刚好抽到一男一女的情况数,即可求出所求的概率. (1)该校七年级书法班共有学生人数是...如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)将Rt△ABC绕点O顺时针旋转90°后得到Rt△A′B′C′,试在图中画出图形Rt△A′B′C′,并写出C′的坐标;
(2)求弧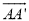 的长.
的长.
解方程:(1)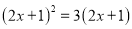 (2)
(2)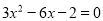
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD= .
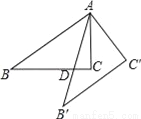
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 .
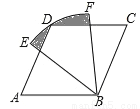
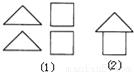
在拼图游戏中,从图(1)的四张纸片中,任取两张纸片,能拼成“房子”如图(2)的概率为 .
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
当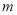 =_______时,方程
=_______时,方程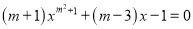 是一元二次方程.
是一元二次方程.
如图所示,二次函数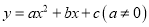 的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②
的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②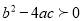 ;③a+c<2-b;④
;③a+c<2-b;④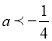 ; ⑤x=-5和x=7时函数值相等.其中正确的结论有 ( )
; ⑤x=-5和x=7时函数值相等.其中正确的结论有 ( )
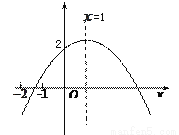
A. 1个 B. 2个 C. 3个 D. 4个
查看答案(2016重庆市)从﹣3,﹣1, 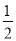 ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组 无解,且使关于x的分式方程
无解,且使关于x的分式方程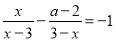 有整数解,那么这5个数中所有满足条件的a的值之和是( )
有整数解,那么这5个数中所有满足条件的a的值之和是( )
A. ﹣3 B. ﹣2 C. ﹣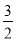 D.
D. 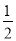
如图,圆O的弦AB垂直平分半径OC,则四边形OACB一定是( )
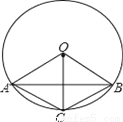
A. 正方形 B. 长方形 C. 菱形 D. 梯形
查看答案关于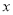 的一元二次方程
的一元二次方程 有实数根,则
有实数根,则 的取值范围是 ( )
的取值范围是 ( )
A.  B.
B. 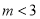 C.
C. 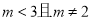 D.
D. 
如图,∠AOB=90°,∠B=30°,△A’OB’可以看作是由△AOB绕点O顺时针旋转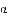
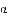
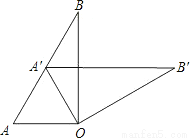
A. 30° B. 45° C. 60° D. 90°
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知x+12平方根是±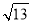 ,2x+y﹣6的立方根是2,求3xy的算术平方根.
,2x+y﹣6的立方根是2,求3xy的算术平方根.
已知:|a﹣1|+|b+2|=0,求2a+b的值.
查看答案如图,一个正五棱柱的底面边长为2cm,高为4cm。
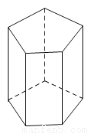
(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有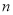 的代数式表示
的代数式表示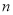 棱柱的顶点数、面数、与棱的条数。
棱柱的顶点数、面数、与棱的条数。
在等式的括号内填上恰当的项,x2﹣y2+8y﹣4=x2﹣(___________).
查看答案如果关于x的多项式x2﹣kx+9是一个完全平方式,那么k=________.
查看答案若a的相反数是﹣3,b的绝对值是4,则a+b=________.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
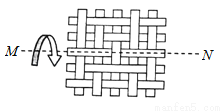
A.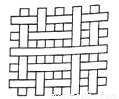 B.
B.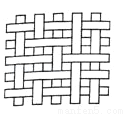 C.
C.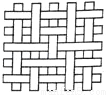 D.
D.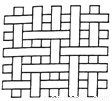
已知函数:①y=ax2;②y=3(x﹣1)2+2;③y=(x+3)2﹣2x2;④y=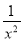 +x.其中,二次函数的个数为( )
+x.其中,二次函数的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案杭州市从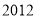 年
年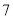 月
月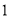 日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
档次 | 全年的用电量 | 电价(单位:元/度) |
第一档 |
|
|
第二档 |
|
|
第三档 |
|
|
(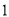 )小王家
)小王家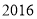 年全年的用电量是
年全年的用电量是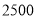 度,请计算小王家这年的电费付了多少元?
度,请计算小王家这年的电费付了多少元?
(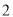 )小李家
)小李家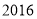 年
年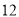 月份这个月的用电量是
月份这个月的用电量是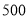 度,小李算出它们家的电费是
度,小李算出它们家的电费是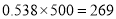 元,而供电局却收了小李家的电费
元,而供电局却收了小李家的电费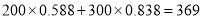 元,你知道其中的奥秘吗?请你来解释下.
元,你知道其中的奥秘吗?请你来解释下.
(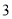 )小张家
)小张家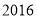 年全年用电量为
年全年用电量为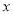 度,请用含
度,请用含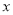 的代数式表示小张家全年应交的总电费,并把结果化简.
的代数式表示小张家全年应交的总电费,并把结果化简.
化简与求值:
(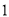 )已知当
)已知当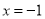 时,代数式
时,代数式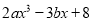 值为
值为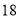 ,求代数式
,求代数式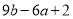 的值.
的值.
(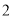 )已知
)已知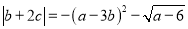 ,代数式
,代数式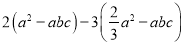 的值.
的值.
(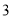 )若多项式
)若多项式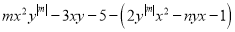 是关于
是关于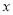 ,
, 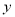 的四次二项式,求代数式
的四次二项式,求代数式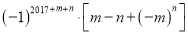 的值.
的值.
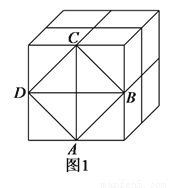
如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形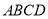 ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.
(3)把正方形 放到数轴上,如图
放到数轴上,如图 ,使得
,使得 与
与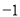 重合,点
重合,点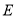 与
与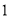 重合,点
重合,点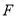 与点
与点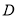 关于
关于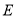 点对称,那么
点对称,那么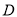 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点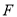 在数轴上表示的数为__________.
在数轴上表示的数为__________.
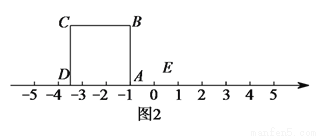
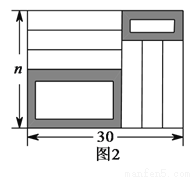
把六张形状大小完全相同的小长方形卡片(其中较短的一边长为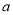 厘米,如图
厘米,如图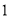 )不重叠地放在一个底面为长方形(长为
)不重叠地放在一个底面为长方形(长为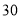 厘米,宽为
厘米,宽为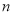 厘米)的盒子底部(如图
厘米)的盒子底部(如图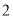 ),盒子底面未被卡片覆盖的部分分别用
),盒子底面未被卡片覆盖的部分分别用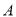 ,
,  表示,请观察图形,回答问题:
表示,请观察图形,回答问题:
(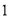 )求矩形
)求矩形 的长和宽(用含
的长和宽(用含 或
或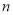 的代数式表示).
的代数式表示).
( )当图中两块长方形阴影部分
)当图中两块长方形阴影部分 ,
, 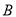 的周长和(用含
的周长和(用含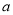 或
或 的代数式表示).
的代数式表示).
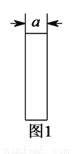
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


 度以内(包括
度以内(包括 度)
度)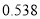
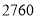 至
至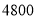 度(包含
度(包含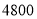 度)
度)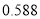
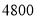 度以上
度以上