��Ŀ����
����������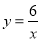 ͼ�����������㣨x1��y1������x2��y2������x3��y3��������x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ��( )
ͼ�����������㣨x1��y1������x2��y2������x3��y3��������x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ��( )
A. y2��y1��y3 B. y1��y2��y3 C. y3��y1��y2 D. y3��y2��y1
A ��������k=6��0�����Է���������ͼ��λ��һ�����ޣ����ҵ�x��0ʱ��y����x���������С������y2��y1��y3. ��ѡA. �㾦����֪��������������ʽ�͵�ĺ�����Ҫ�Ƚ��������С���������ν�ϣ�����ͼ������ʽ��бȽ�.һ��������װ�д�С����״��ͬ���ĸ������к���1��������1��������2����С������һ���Żأ�������һ���������ζ���������ĸ����ǣ� ��
A. 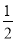 B.
B. 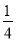 C.
C. 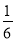 D.
D. 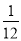
��ͼ����O�ǡ�ABC�����Բ����OCB��40�����A�Ķ�������( )
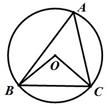
A. 60�� B. 50�� C. 40�� D. 30��
�鿴��������ͼ���У�������Գ�ͼ�Σ��������ĶԳ�ͼ�ε��ǣ� ��
A.  B .
B . C .
C . D.
D. 
��֪���������� �����н��۲���ȷ����
�����н��۲���ȷ����
A��ͼ��ؾ�����(-1,2) B��y��x�����������
C��ͼ���ڵڶ�����������D����x��1����y��-2
�鿴���ھ���ABCD�У�AB=6cm��BC=12cm����P�ӵ�A��������AB�����B��ÿ��1cm���ٶ��ƶ���ͬʱ��Q�ӵ�B������BC�����C��ÿ��2cm���ٶ��ƶ�P��Q�����ڷֱ�B��C������ֹͣ�ƶ����������ƶ���ʱ��Ϊt�룬�ش��������⣺
��1����ͼ1����tΪ����ʱ����PBQ���������5cm2��
��2����ͼ2����t= ��ʱ�����жϡ�DPQ����״����˵�����ɣ�
��ʱ�����жϡ�DPQ����״����˵�����ɣ�
��3����ͼ3����QΪԲ�ģ�PQΪ�뾶����Q��
�����˶������У��Ƿ����������tֵ��ʹ��Q�������ı���DPQC��һ�ߣ�������ڵ�ֱ�ߣ����У������ڣ����tֵ���������ڣ���˵�����ɣ�
������Q���ı���DPQC�����������㣬��ֱ��д��t��ȡֵ��Χ��

- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���һ�������������Ϊ����֮һ�������ԭ�����йص������⣬���ǰ�����Ϊԭ�����һ�����������⣮���磬ԭ�����ǡ������ε����߳��ֱ�Ϊ3��4������ε��ܳ���������ܳ�����14������һ����������������ǡ������ε��ܳ�Ϊ14����һ�߳�Ϊ3������һ�ߵij�����Ҳ�����ǡ������ε��ܳ�Ϊ14���������������ֵ�����ȵȣ�
��1����A=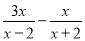 ��B=
��B=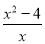 ����A��B�Ļ���
����A��B�Ļ���
��2�������1����һ�����������⣬�����������⣮
��1��2x+8;(2) �������������������1����A��B��Ӧ�Ĵ���ʽ����A��B�����з�ʽ�����㣬���ɵõ�A��B�Ļ��� ��2���������⣬��֪���Ը�ΪA��B�Ļ����Լ�A��ֵ����B��ֵ�� �����������1�� A��B==2x+8�� ��2�������������ǣ���֪A��B=2x+8��A=����B��ֵ�� B=��2x+8���£���=��2x+8����=�� ���㣺��ʽ�Ļ�����㣮��Ҫ��������и��⣺
��1����֪ʵ��a��b���㣨a+b��2=1����a��b��2=9����a2+b2��ab��ֵ��
��2����֪��2015��a����2016��a��=2047������a��2015��2+��2016��a��2��ֵ��
�鿴�����Ƚ���ʽ������ѡ��һ���ʵ�����������ֵ����1��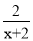 ����
����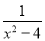 ��
��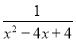 ��
��
�ⷽ��
��1��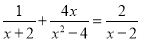 ��2��
��2��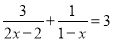
����
��1���Ȼ�������ֵ����2x��1����x+2����2x��x+1����x=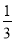 ��
��
��2����֪��a+b=4��ab=3����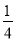 a3b+
a3b+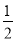 a2b2+
a2b2+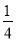 ab3��ֵ��
ab3��ֵ��
��ʽ�֡�������
��1����a+b��2+6��a+b��+9��������������������������2����x��y��2��9��x+y��2��
��3��a2��x��y��+b2��y��x���� ��4��(x2��5)2��8(5��x2)��16.
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ��Ϊ�˹��ƺӵĿ��ȣ��ںӵĶ�ѡ��һ��Ŀ���P���ڽ���ȡ��Q��S��ʹ��P��Q��S��һ��ֱ���ϣ���ֱ��PS��Ӵ�ֱ���ڹ���S����PS��ֱ��ֱ��a��ѡ���ʵ��ĵ�T��PT�����Q����PS��ֱ��ֱ��b�Ľ���ΪR�����QS=60m��ST=120m��QR=80m����ӵĿ���PQΪ��������
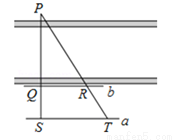
A. 40m B. 60m C. 120m D. 180m
C ���������������QR||ST,����=, �� ����ѡC.��֪��P(1��2)�ڷ���������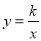 ��ͼ���ϣ���P��
��ͼ���ϣ���P��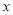 ��Ĵ��ߣ�����ΪM�����OPM�����Ϊ��������
��Ĵ��ߣ�����ΪM�����OPM�����Ϊ��������
A. 2 B. 4 C. 8 D. 1
�鿴�������Ϸ���1���������1��Բ���壬����ͼ��ʾ�ķ�ʽ�ڷ���һ��������ͼ�ǣ� ��
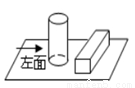
A.  B.
B.  C.
C.  D.
D. 
�����ж���ȷ���ǣ�������
A. ��AB��BC���� ABCD������ B. ��AC��BD����
ABCD������ B. ��AC��BD���� ABCD��������
ABCD��������
C. ��AC=BD����  ABCD�Ǿ��� D. ��AB=AD����
ABCD�Ǿ��� D. ��AB=AD���� ABCD��������
ABCD��������
��ͼ��ͬһʱ��ѧУ��һ��������˵�Ӱ�ӣ��������Ϊ3�ף��������Ӱ�ӳ�Ϊ1.2�ף���˵ĸ߶�Ϊ5�ף�������Ӱ�ӳ�Ϊ�� ��
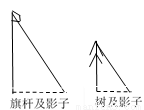
A. 4�� B. 2�� C. 1.8�� D. 3.6��
�鿴������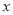 ��һԪ���η���
��һԪ���η���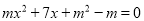 �ij�����Ϊ0����
�ij�����Ϊ0���� ��ֵ���ڣ� ��
��ֵ���ڣ� ��
A. 1 B. 2 C. 0��1 D. 0
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
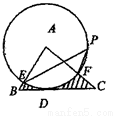
��ͼ���ڡ�ABC�У�BC��4���Ե�AΪԲ�ģ�2Ϊ�뾶�ġ�A��BC�����ڵ�D����AB��E����AC��F����P�ǡ�A�ϵ�һ�㣬�ҡ�EPF��40�㣬��ͼ����Ӱ���ֵ������__________��������� ��
��
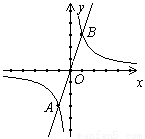
��ͼ������������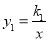 ������������y2=k2x ��ͼ����A��-1��-3����B��1��3�����㣬��
������������y2=k2x ��ͼ����A��-1��-3����B��1��3�����㣬��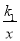 ��k2x����x��ȡֵ��Χ��___________________.
��k2x����x��ȡֵ��Χ��___________________.
��֪��A(��1��y1)��B(2��y2)����˫����y�� �ϣ���y1��y2����m��ȡֵ��Χ��______________
�ϣ���y1��y2����m��ȡֵ��Χ��______________
��������y��x2��2x��3��x��ֱ���A��B���㣬��AB�ij�Ϊ ______��
�鿴��ֱ��y=x+3����һ��P(3,a)�����P����ԭ��ĶԳƵ� Ϊ___________.
Ϊ___________.
��ͼ����������������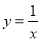 ��
��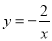 ��ͼ��ֱ���l1��l2�����P��l1�ϣ�PC��x�ᣬ����ΪC����l2�ڵ�A��PD��y�ᣬ����ΪD����l2�ڵ�B�����PAB�����Ϊ��������
��ͼ��ֱ���l1��l2�����P��l1�ϣ�PC��x�ᣬ����ΪC����l2�ڵ�A��PD��y�ᣬ����ΪD����l2�ڵ�B�����PAB�����Ϊ��������
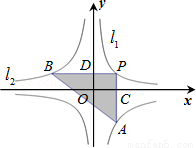
A. 3 B. 4 C. 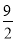 D. 5
D. 5
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
ijͬѧ������㷨�����κ���y=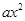 +bx+c��ͼ��ʱ���г�������ı���
+bx+c��ͼ��ʱ���г�������ı���
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | ��11 | ��2 | 1 | ��2 | ��5 | �� |
���ڴ��ģ������������һ��yֵ��������������ֵ�ǣ� ��.
A����11 B����2 C��1 D����5
D�� ��������������������ݹ��ڶԳ���ԳƵ��Ա�����Ӧ�ĺ���ֵ��ȣ��ɵô𰸣��ɺ���ͼ����ڶԳ���Գƣ��ã���1����2������0��1������1����2���ں���ͼ���ϣ��ѣ���1����2������0��1������1����2�����뺯������ʽ����a-b+c=-2��c=1��a+b+c=-2�����a=-3��b=0��c=1�����Ժ�������ʽΪy=+1��x=2ʱy=��11. ��ѡ��D�� ���㣺���κ�����ͼ�� ...��Բ�ĵ����Ϊ16��cm2��ĸ�߳�Ϊ12cm�������IJ���չ��ͼ��Բ�Ľ�Ϊ( )
A. 240�� B. 120�� C. 180�� D. 90��
�鿴����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����ôһ�κ���y=bx+c�ͷ���������y=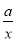 ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
��ͼ��������ABCD�ڽ��ڡ�O����O��ֱ��Ϊ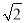 ���ף��������Բ����������һ�����ӣ���������������ABCD�ڵĸ����ǣ� ����
���ף��������Բ����������һ�����ӣ���������������ABCD�ڵĸ����ǣ� ����
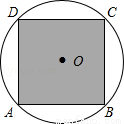
A��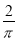 B��
B��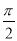 C��
C��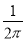 D��
D��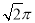
��ͼ��AB�ǡ�O��ֱ������CD��AB������ΪE�����AB=10��CD=8����ô�߶�OE�ij�Ϊ�� ��
A��6 B��5 C��4 D��3
�鿴������������ ͼ�����������㣨x1��y1������x2��y2������x3��y3��������x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ��( )
ͼ�����������㣨x1��y1������x2��y2������x3��y3��������x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ��( )
A. y2��y1��y3 B. y1��y2��y3 C. y3��y1��y2 D. y3��y2��y1
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
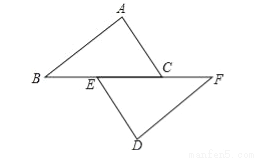
��ͼ����֪��B��E��C��F��һ��ֱ���ϣ�AB=DF��AC=DE����A=��D��
��1����֤��AC��DE��
��2����BF=13��EC=5����BC�ij���
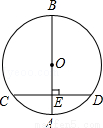
ֱ��y=kx+4�����㣨1��2������ʽkx+4��0�Ľ⼯��
�鿴��ijУ��չ����Լÿһ��ˮ�����Ϊ���˽չ���һ����������Լ��ˮ�IJ������Ӱ��꼶��400��ͬѧ��ѡ��20��ͬѧͳ���˽���Լ�ͥһ���µĽ�ˮ��������±���
��ˮ��m3�� | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
��ͥ�������� | 2 | 4 | 6 | 7 | 1 |
�ֱ������20����ͥ��ˮ����λ�������������������400��ͬѧ�ļ�ͥһ���½�Լ��ˮ��������Լ�Ƕ���m3��
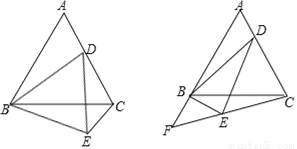
�鿴����ͼ����ABC�͡�ABD�У���C=��D=Rt�ϣ�E��BC���ϵ����ߣ�����˵��CE=DE�����ɣ�
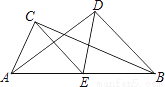
��ͼ���ı���ABCD�У�E����AD�ϣ����С�BAE=��BCE=��ACD=90�㣬��BC=CE����֤����ABC���DECȫ�ȣ�
�������x�IJ���ʽk��x+6��0����������Ϊ1��2��3����ôk��ȡֵ��Χ�Ƕ��٣�
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��M��a����5�����N����2��b������x��Գƣ���a+b=________��
3 ������������������ߵ�M��a��-5�����N��-2��b������x��Գƣ� ��a=-2��b=5�� ��a+b=-2+5=3����һ�����dz߰���ͼ��ʾ�ķ�ʽ���ã�ʹ��30��ǵ����dzߵĶ�ֱ�DZߺͺ�45��ǵ����dzߵ�һ��ֱ�DZ��غϣ����1�Ķ������� ����
���и�ʽ��y=0.5x��2����y=|2x|����3y+5=x����y2=2x+8�У�y��x�ĺ�������_______ (ֻ����ţ�
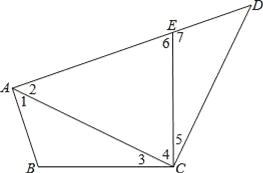
�鿴����ͼ��գ���֪��ͼ��AD��BC��D��EG��BC��G����E=��1��
��֤��ADƽ�֡�BAC��
֤������AD��BC��D��EG��BC��G�� ��֪ ��
���ADC=90�㣬��EGC=90�㣨___________��
���ADC=��EGC������������
��AD��EG��_____________��
���1=��2��___________��
��E=��3��___________��
�֡ߡ�E=��1�� ��֪��
���2=��3��___________��
��ADƽ�֡�BAC��___________����
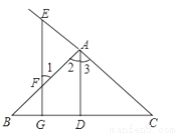
Ϊ�˹���������������������������ȴ������д���30�������ϱ�ǣ�Ȼ��Ź�����������һ��ʱ�䣬���б�ǵ�����ȫ�������Ⱥ�У��ٴ���200���㣬�������д���ǵ�����5�����������й�����________���㣮
�鿴��һ�κ���y=��m2��4��x+��1��m����y=��m��1��x+m2��3��ͼ����y��ֱ��ڵ�P�͵�Q������P���Q����x��Գƣ���m=________
�鿴�� ��������- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ֱ��y��3x+6��ֱ��y��2x+4�Ľ�������Ϊ��a �� b�������Ϊ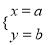 �ķ������ǣ�������
�ķ������ǣ�������
A. 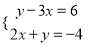 B.
B. 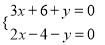 C.
C. 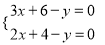 D.
D. 
��ͼ����֪�ȱߡ�ABC�У�DΪ��AC��һ�㣮
��1����BDΪ�����ȱߡ�BDE������CE����֤��AD=CE��
��2�������BDΪб����Rt��BDE���ҡ�BDE=30�㣬����CE���ӳ�����AB���ӳ��߽���F�㣬��֤��AD=BF��
�Ķ�����IJ��ϣ��ش����⣺
�ⷽ��x4��5x2+4=0������һ��һԪ�Ĵη��̣����ݸ÷��̵��ص㣬���Ľⷨͨ���ǣ�
��x2=y����ôx4=y2������ԭ���̿ɱ�Ϊy2��5y+4=0 �٣����y1=1��y2=4��
��y=1ʱ��x2=1����x=��1��
��y=4ʱ��x2=4����x=��2��
��ԭ�������ĸ�����x1=1��x2=��1��x3=2��x4=��2��
����ԭ���̵õ����̢ٵĹ����У����û�Ԫ���ﵽ���ε�Ŀ�ģ���������ѧ��ת��˼�룬���������������ⷽ��
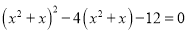
�̳�ij����Ʒƽ��ÿ�������20����ÿ��ӯ��40Ԫ��Ϊ�˾�����ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣�ÿ����Ʒÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2����
��1�����̳�ƽ��ÿ��Ҫӯ��1200Ԫ��ÿ������Ӧ���۶���Ԫ����ʱ��ÿ������ӯ������Ԫ��
��2��ÿ���������۶���Ԫ���̳�ƽ��ÿ��ӯ����ࣿ
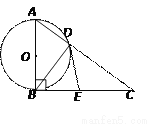
�鿴����ͼ����֪R t��ABC����ABC��90�㣬��ֱ�DZ�ABΪֱ����O����б��AC�ڵ�D������BD��
��1����AB��3��BC��4�����BD�ij���
��2��ȡBC���е�E������ED����֤��ED���O���У�
ijУ��ίΪ�������롰����֪����ȫ���鷨�������ֳ���������ѧУѧ�������黭��Ʒ������3�·ݾ����ˡ��黭�����������������ɼ�����ΪA��B��C��D��E����ȼ�����У���꼶�鷨��ȫ��ѧ���μ���ѧУ�ı�������������������Ƴ�����������������ͳ��ͼ�������ͼ����Ϣ������������⣮
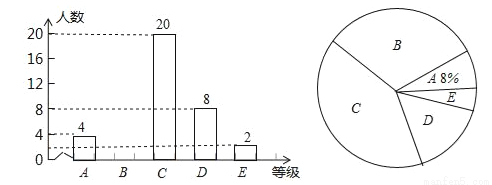
��1����У���꼶�鷨��� ��ѧ��������ͳ��ͼ��C�ȼ�����Ӧ���ε�Բ�Ľǵ��� �ȣ�����ȫ����ͳ��ͼ��
��2��A�ȼ���4��ѧ������2��������2��Ů�����ִ�������ѡȡ2��ѧ���μӡ�����֪����ȫ���鷨�������ֳ��������������б�������״ͼ�ķ��������ǡ��ѡ��1��������1��Ů���ĸ��ʣ�
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�������ϣ���A��ʾ�����ǩ�5����C��ʾ������4����AB=2BC�����B�������ϱ�ʾ�����ǣ� ��
A. 1��13 B. 1 C. 9 D. ��2��10
A ��������������������ڵ�A��ʾ�����ǩ�5����C��ʾ������4�����߶�AC�ij���Ϊ9����AB=2BC��������������ٵ�B��C���ұߣ���B��C����ߣ� �������� �ߵ�A��ʾ�����ǩ�5����C��ʾ������4�� ��AC=4������5��=9�� �֡�AB=2BC�� ��ٵ�B��C���ұߣ�������ӦΪ4+9=13�� ��B��C����ߣ�������ӦΪ4��9��=4��3=1�� �ʵ�B����...�ѷ���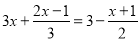 ȥ��ĸ��ȷ���ǣ�������
ȥ��ĸ��ȷ���ǣ�������
A. 18x��2��2x��1����18��3��x��1�� B. 3x����2x��1����3����x��1��
C. 18x����2x��1����18����x��1�� D. 3x��2��2x��1����3��3��x��1��
�鿴��һ����Ϊ19cm����Ϊ18cm�ij����Σ��������������ηֳ����ɸ�������Ҫ�������εı߳�Ϊ����������ô�ó��������ٿɷֳ������εĸ�����������
A. 5�� B. 6�� C. 7�� D. 8��
�鿴���������������У���������ǣ�������
A. 1+����2�� B. 1������2�� C. 1������2�� D. 1�£���2��
�鿴����2016�Ĵ�ʡ�ϳ��У����������5����Ϊ+5����ô������3����Ϊ��������
A. +3 B. ��3 C. 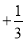 D.
D. 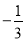
����a+1��2+|b��2|=0������a��x2y+xy2����b��x2y��xy2���Ľ��Ϊ�� ��
A��3x2y B����3x2y+xy2 C����3x2y+3xy2 D��3x2y��xy2
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������

