题目内容
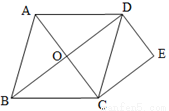
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
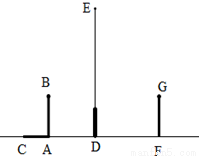
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案在一次朋友聚餐中,有A、B、C、D四种素菜可供选择,小明从中选择一种,小莉也从中选择一种(与小明选择的不相同),请利用列表或树状图的方法求出A与B两种素菜被选中的概率.
查看答案直线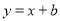 与反比例函数
与反比例函数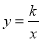 (
(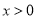 )的图象交于点A(1,2),求这两个函数的表达式.
)的图象交于点A(1,2),求这两个函数的表达式.
解一元二次方程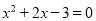
如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案若有理数a的值在﹣1与0之间,则a的值可以是( )
A. ﹣2 B. 1 C. 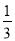 D.
D. 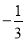
下列运算正确的是( )
A. 3a+2b=5ab B. 3a2b﹣3ba2=0 C. 3x2+2x3=5x5 D. 5y2﹣4y2=1
查看答案下列各组是同类项的是( )
A. a3与a2 B. 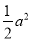 与2a2 C. 2xy与2y D. 3与a
与2a2 C. 2xy与2y D. 3与a
﹣3的相反数是( )
A. 3 B. ﹣3 C. - D.
D. 
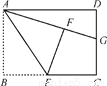
如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AEF,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,∠DAF=________.
反比例函数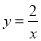 中自变量x的取值范围是________。
中自变量x的取值范围是________。
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=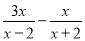 ,B=
,B=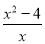 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
(1)2x+8;(2) 【解析】试题分析:(1)把A和B对应的代数式代入A×B,进行分式的运算,即可得到A与B的积; (2)读懂题意,已知可以改为A×B的积,以及A的值,求B的值. 试题解析:(1) A×B==2x+8; (2)“逆向”问题是:已知A×B=2x+8,A=,求B的值. B=(2x+8)÷()=(2x+8)×=. 考点:分式的混合运算.按要求完成下列各题:
(1)已知实数a、b满足(a+b)2=1,(a﹣b)2=9,求a2+b2﹣ab的值;
(2)已知(2015﹣a)(2016﹣a)=2047,试求(a﹣2015)2+(2016﹣a)2的值.
查看答案请先将下式化简,再选择一个适当的数代入求值.(1﹣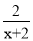 )﹣
)﹣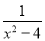 ÷
÷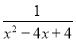 .
.
解方程
(1)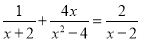 (2)
(2)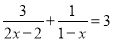
计算
(1)先化简,再求值:(2x﹣1)(x+2)﹣2x(x+1),x=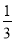 .
.
(2)已知:a+b=4,ab=3,求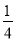 a3b+
a3b+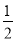 a2b2+
a2b2+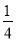 ab3的值.
ab3的值.
因式分【解析】
(1)(a+b)2+6(a+b)+9; (2)(x﹣y)2﹣9(x+y)2;
(3)a2(x﹣y)+b2(y﹣x). (4)(x2-5)2+8(5-x2)+16.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若关于x的分式方程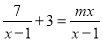 无解,则实数m的值是( )
无解,则实数m的值是( )
A. x=0或1 B. x=1或3 C. x=3或7 D. x=0或3
C 【解析】试题解析:方程去分母得:7+3(x-1)=mx, 整理,得(m-3)x=4, 当整式方程无解时,m-3=0,m=3; 当整式方程的解为分式方程的增根时,x=1, ∴m-3=4,m=7, ∴m的值为3或7. 故选C. 点睛:分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
A. 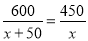 B.
B. 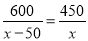 C.
C. 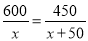 D.
D. 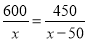
能使分式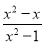 的值为零的所有x的值是( )
的值为零的所有x的值是( )
A. x=1 B. x=0 C. x=0或x=1 D. x=0或x=±1
查看答案若把分式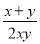 中的x和y都扩大3倍,那么分式的值( )
中的x和y都扩大3倍,那么分式的值( )
A. 扩大3倍 B. 不变 C. 缩小3倍 D. 缩小6倍
查看答案与分式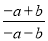 相等的是( )
相等的是( )
A. 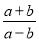 B.
B. 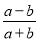 C.
C. 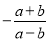 D.
D. 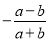
任意给定一个非零数,按下列程序计算,最后输出的结果是( )
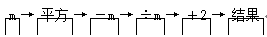
A. m B. m-2 C. m+1 D. m2+1
查看答案 试题属性- 题型:单选题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
计算(ab2)3的结果,正确的是( )
A. a3b6 B. a3b5 C. ab6 D. ab5
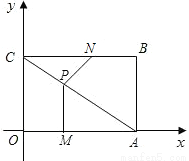
A 【解析】试题解析:(ab2)3=a3?(b2)3=a3b6. 故选A. 点睛:积的乘方等于每一个因式分别乘方,再把所得的幂相乘.如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了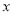 秒.
秒.
(1)当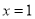 时,求PC的长;
时,求PC的长;
(2)当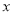 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?
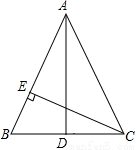
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.
(1)求证:△ABD∽△CBE;
(2)若BD=3,BE=2,求AC的值.
水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低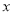 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含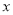 的代数式表示);
的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
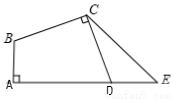
查看答案如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.

函数 是
是 关于
关于 的反比例函数,则
的反比例函数,则 _______.
_______.
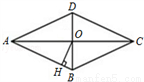
如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=_____.
一个直角三角形斜边上的高与中线分别是5㎝和6㎝,则它的面积是______ 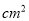 .
.
反比例函数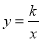 经过点(-2,1),则一次函数
经过点(-2,1),则一次函数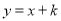 的图象经过点(-1,_____).
的图象经过点(-1,_____).
方程(x+2)2=x+2的解是 ____________________.
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
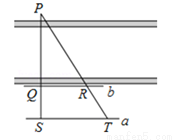
A. 40m B. 60m C. 120m D. 180m
C 【解析】由题意得QR||ST,所以=, , 所以选C.已知点P(1,2)在反比例函数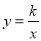 的图象上,过P作
的图象上,过P作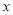 轴的垂线,垂足为M,则△OPM的面积为( )
轴的垂线,垂足为M,则△OPM的面积为( )
A. 2 B. 4 C. 8 D. 1
查看答案桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是( )
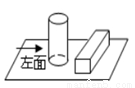
A. 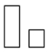 B.
B. 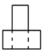 C.
C. 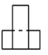 D.
D. 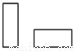
以下判定正确的是( )
A. 若AB⊥BC,则 ABCD是菱形 B. 若AC⊥BD,则
ABCD是菱形 B. 若AC⊥BD,则 ABCD是正方形
ABCD是正方形
C. 若AC=BD,则  ABCD是矩形 D. 若AB=AD,则
ABCD是矩形 D. 若AB=AD,则 ABCD是正方形
ABCD是正方形
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
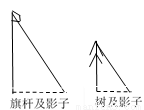
A. 4米 B. 2米 C. 1.8米 D. 3.6米
查看答案关于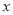 的一元二次方程
的一元二次方程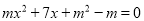 的常数项为0,则
的常数项为0,则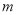 的值等于( )
的值等于( )
A. 1 B. 2 C. 0或1 D. 0
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
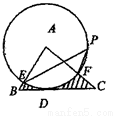
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是__________(结果保留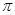 )
)
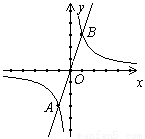
如图,反比例函数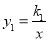 和正比例函数y2=k2x 的图象交于A(-1,-3)、B(1,3)两点,若
和正比例函数y2=k2x 的图象交于A(-1,-3)、B(1,3)两点,若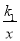 >k2x,则x的取值范围是___________________.
>k2x,则x的取值范围是___________________.
已知点A(-1,y1)、B(2,y2)都在双曲线y= 上,且y1>y2,则m的取值范围是______________
上,且y1>y2,则m的取值范围是______________
若抛物线y=x2-2x-3与x轴分别交于A,B两点,则AB的长为 ______.
查看答案直线y=x+3上有一点P(3,a),则点P关于原点的对称点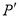 为___________.
为___________.
如图,两个反比例函数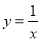 和
和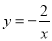 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为( )
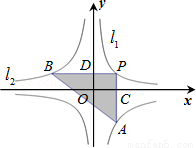
A. 3 B. 4 C. 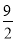 D. 5
D. 5
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若直线y=3x+6与直线y=2x+4的交点坐标为(a , b),则解为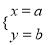 的方程组是( )
的方程组是( )
A. 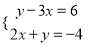 B.
B. 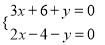 C.
C. 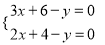 D.
D. 
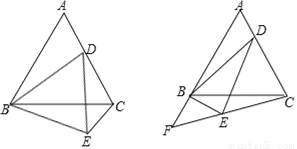
如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;
阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程
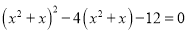
商场某种商品平均每天可销售20件,每件盈利40元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?此时,每件衬衫盈利多少元?
(2)每件衬衫降价多少元,商场平均每天盈利最多?
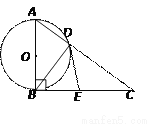
查看答案如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.
某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.
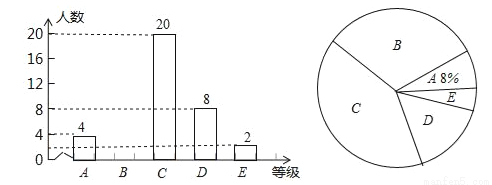
(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

