题目内容
10.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.(1)若a=2,b=4,则c=2$\sqrt{5}$;
(2)若a=2,c=4,则b=2$\sqrt{3}$;
(3)若c=26,a:b=5:12,则a=10,b=24.
分析 根据题意画出图形,再根据勾股定理求解即可.
解答 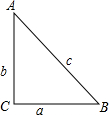 解:如图,
解:如图,
(1)∵a=2,b=4,
∴c=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$;
(2)∵a=2,c=4,
∴b=$\sqrt{{4}^{2}-{2}^{2}}$=$\sqrt{12}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$;
(3)∵c=26,a:b=5:12,
∴设a=5x,则b=12x,
∵a2+b2=c2,即(5x)2+(12x)2=262,解得x=2,
∴a=10,b=24.
故答案为:10,24.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
20.有一人患了红眼病,经过两轮传染后共有144人患了红眼病,那每轮传染中平均一个人传染的人数为( )人.
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
18. 如图所示,在数轴上有四个点A、B、C、D,其中表示-2的相反数的是( )
如图所示,在数轴上有四个点A、B、C、D,其中表示-2的相反数的是( )
 如图所示,在数轴上有四个点A、B、C、D,其中表示-2的相反数的是( )
如图所示,在数轴上有四个点A、B、C、D,其中表示-2的相反数的是( )| A. | 点 A | B. | 点B | C. | 点C | D. | 点D |
5.下列计算正确的是( )
| A. | (x2)3=x5 | B. | $\sqrt{9}$=3 | C. | x2+x2=x4 | D. | 3x•3x2=6x3 |
2. 如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )
如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )
 如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )
如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 50° |
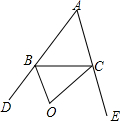 如图,O是外角∠DBC的平分线BO与外角∠ECB的平分线CO的交点,则∠BOC与∠A的关系是∠BOC=90°+$\frac{1}{2}$∠A.
如图,O是外角∠DBC的平分线BO与外角∠ECB的平分线CO的交点,则∠BOC与∠A的关系是∠BOC=90°+$\frac{1}{2}$∠A.