题目内容
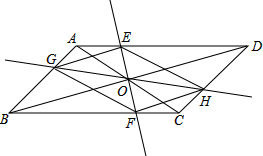 在?ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.
在?ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.(1)如图,试证明OE=OF;
(2)如图,试判断四边形EGFH的形状,并说明理由.
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)证明△ODE≌△OBF即可证得;
(2)OE=OF,同理可以证得OG=OH,根据对角线互相平分的四边形是平行四边形即可判断出EGFH是平行四边形.
(2)OE=OF,同理可以证得OG=OH,根据对角线互相平分的四边形是平行四边形即可判断出EGFH是平行四边形.
解答:解:(1)∵?ABCD中,OD=OB,AD∥BC,
∴∠ADO=∠CBO,
在△ODE和△OBF中,
,
∴△ODE≌△OBF,
∴OE=OF;
(2)四边形EGFH是平行四边形.
证明:同(1)可证:GO=HO,
∵EO=FO,GO=HO;
∴四边形EGFH是平行四边形.
∴∠ADO=∠CBO,
在△ODE和△OBF中,
|
∴△ODE≌△OBF,
∴OE=OF;
(2)四边形EGFH是平行四边形.
证明:同(1)可证:GO=HO,
∵EO=FO,GO=HO;
∴四边形EGFH是平行四边形.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定和性质,正确证明OE=OF是关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图,过?ABCD的顶点D,C分别向对边AB所在直线作垂线DE和CF,垂足分别为点E,F,求证:AE=BF.
如图,过?ABCD的顶点D,C分别向对边AB所在直线作垂线DE和CF,垂足分别为点E,F,求证:AE=BF. 如图是一个粮仓(圆锥与圆柱组合体)的示意图,请画出它的三视图.
如图是一个粮仓(圆锥与圆柱组合体)的示意图,请画出它的三视图. 如图,在?ABCD中,对角线AC与BD交于点O,OE⊥AC交AD于点E,△CDE的周长为12,求?ABCD的周长.
如图,在?ABCD中,对角线AC与BD交于点O,OE⊥AC交AD于点E,△CDE的周长为12,求?ABCD的周长.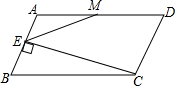 如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.
如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM. 如图,在?ABCD中,延长AD到点E,使得DE=AD,连结BE.求证:CD与BE互相平分.
如图,在?ABCD中,延长AD到点E,使得DE=AD,连结BE.求证:CD与BE互相平分.