题目内容
如图，在?ABCD中，延长AD到点E，使得DE=AD，连结BE．求证：CD与BE互相平分．考点：平行四边形的判定与性质
专题：证明题
分析：连接DB，EC，由四边形ABCD为平行四边形得到对边平行且相等，再由DE=AD，等量代换得到ED=BC，由ED与BC平行，得到四边形BDEC为平行四边形，根据平行四边形的对角线互相平分即可得证．
解答：
证明：连接DB，EC，
∵四边形ABCD为平行四边形，
∴AD∥BC，且AD=BC，
∵DE=AD，
∴DE∥BC，DE=BC，
∴四边形BDEC为平行四边形，
∴CD与BE互相平分．
证明：连接DB，EC，∵四边形ABCD为平行四边形，
∴AD∥BC，且AD=BC，
∵DE=AD，
∴DE∥BC，DE=BC，
∴四边形BDEC为平行四边形，
∴CD与BE互相平分．
点评：此题考查了平行四边形的判定与性质，熟练掌握平行四边形的判定与性质是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
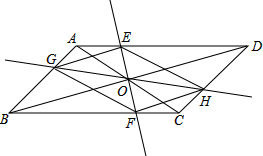在?ABCD中，AC，BD交于点O，过点O作直线EF，GH，分别交平行四边形的四条边于E，G，F，H四点，连接EG，GF，FH，HE．
如图是一块蛋糕，表面的形状是平行四边形，且内有一个平行四边形的孔．你能一刀将它切成面积相等的两块吗？请说出你的切法，并画出示意图．
如图，在?ABCD中，E，F分别是AB，CD的中点，G，H分别是AF，CE的中点，连结EG，FH．
如图是由16个边长为1的正方形拼成的图案，任意连结这些小格点的三个顶点可得到一些三角形．与A，B点构成直角三角形ABC的顶点C的位置有