题目内容
试说明:两个连续奇数的平方差是这两个连续奇数和的2倍.
考点:因式分解的应用
专题:证明题
分析:设两个连续奇数为2n-1,2n+1(n为整数),利用平方差公式分解(2n+1)2-(2n-1)2得到(2n+1+2n-1)(2n+1-2n+1),整理后即可得到结论.
解答:证明:设两个连续奇数为2n-1,2n+1(n为整数),
(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=2[(2n+1)+(2n-1)],
即两个连续奇数的平方差是这两个连续奇数和的2倍.
(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=2[(2n+1)+(2n-1)],
即两个连续奇数的平方差是这两个连续奇数和的2倍.
点评:本题考查了因式分解的运用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
下列各式中,正确的是( )
A、已知ab>0,则
| ||||||||||||||||
B、2
| ||||||||||||||||
C、
| ||||||||||||||||
D、
|
 如图所示是一个由若干个小立方体叠成的几何体的俯视图,每个小方格中的数字表示该位置上重叠的小立方体的个数,请你画出它的主视图和左视图.
如图所示是一个由若干个小立方体叠成的几何体的俯视图,每个小方格中的数字表示该位置上重叠的小立方体的个数,请你画出它的主视图和左视图. 如图,在一间黑暗的屋子里用一盏白炽灯照一个球.
如图,在一间黑暗的屋子里用一盏白炽灯照一个球. 如图,已知反比例函数
如图,已知反比例函数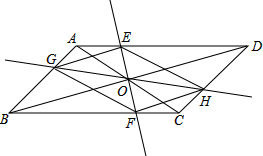 在?ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.
在?ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.

