题目内容
如图，在?ABCD中，对角线AC与BD交于点O，OE⊥AC交AD于点E，△CDE的周长为12，求?ABCD的周长．考点：平行四边形的性质
专题：
分析：首先判断OE是AC的垂直平分线，从而得出EA=EC，再由△CDE的周长为12，可得AD+DC=12，这样即可求出?ABCD的周长．
解答：解：∵四边形ABCD是平行四边形，
∴OA=OC，
又∵OE⊥AC，
∴OE是AC的垂直平分线，
∴EA=EC，
∵△CDE的周长为12，
∴EA+ED+DC=12，
∴?ABCD的周长=2（AD+DC）=24．
∴OA=OC，
又∵OE⊥AC，
∴OE是AC的垂直平分线，
∴EA=EC，
∵△CDE的周长为12，
∴EA+ED+DC=12，
∴?ABCD的周长=2（AD+DC）=24．
点评：本题考查了平行四边形的性质，解答本题注意掌握中垂线的性质及平行四边形对边相等、对角线互相平分的性质．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
如图所示的平面图的比例尺是1：5000，根据图中所示的尺寸（单位：cm）．
为了了解某校九年级学生体育测试成绩情况，现从中随机抽取部分学生的体育成绩统计如表，扇形统计图中的圆心角θ为36°．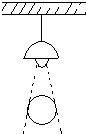
如图，在一间黑暗的屋子里用一盏白炽灯照一个球．
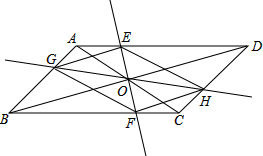在?ABCD中，AC，BD交于点O，过点O作直线EF，GH，分别交平行四边形的四条边于E，G，F，H四点，连接EG，GF，FH，HE．
请在图中作出小鱼旋转的图形．