题目内容
把下列各式分解因式:
(1)-4x3+16x2-26x;
(2)mn(m-n)-m(n-m);
(3)5(x-y)3+10(y-x)2;
(4)3x2+6xy+3y2;
(5)9(m+n)2-16(m-n)2;
(6)m4-16n4.
(1)-4x3+16x2-26x;
(2)mn(m-n)-m(n-m);
(3)5(x-y)3+10(y-x)2;
(4)3x2+6xy+3y2;
(5)9(m+n)2-16(m-n)2;
(6)m4-16n4.
考点:提公因式法与公式法的综合运用
专题:计算题
分析:(1)原式提取公因式即可得到结果;
(2)原式变形后,提取公因式即可得到结果;
(3)原式变形后,提取公因式即可得到结果;
(4)原式提取3,再利用完全平方公式分解即可;
(5)原式利用平方差公式分解即可;
(6)原式利用平方差公式分解即可.
(2)原式变形后,提取公因式即可得到结果;
(3)原式变形后,提取公因式即可得到结果;
(4)原式提取3,再利用完全平方公式分解即可;
(5)原式利用平方差公式分解即可;
(6)原式利用平方差公式分解即可.
解答:解:(1)-4x3+16x2-26x=-2x(2x2-8x+13);
(2)mn(m-n)-m(n-m)=mn(m-n)+m(m-n)=(m-n)(mn+m);
(3)5(x-y)3+10(y-x)2=5(x-y)3+10(x-y)2=5(x-y)2(x-y+2);
(4)3x2+6xy+3y2=3(x2+2xy+y2)=3(x+y)2;
(5)9(m+n)2-16(m-n)2=[3(m+n)+4(m-n)][3(m+n)-4(m-n)]=(7m-n)(-m+7n);
(6)m4-16n4=(m2+4n2)(m2-4n2)=(m2+4n2)(m+2n)(m-2n).
(2)mn(m-n)-m(n-m)=mn(m-n)+m(m-n)=(m-n)(mn+m);
(3)5(x-y)3+10(y-x)2=5(x-y)3+10(x-y)2=5(x-y)2(x-y+2);
(4)3x2+6xy+3y2=3(x2+2xy+y2)=3(x+y)2;
(5)9(m+n)2-16(m-n)2=[3(m+n)+4(m-n)][3(m+n)-4(m-n)]=(7m-n)(-m+7n);
(6)m4-16n4=(m2+4n2)(m2-4n2)=(m2+4n2)(m+2n)(m-2n).
点评:此题考查了提公因式法与公式法的综合运用,熟练掌握公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数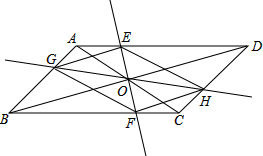 在?ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.
在?ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE. 如图,已知O为坐标原点,将直线y=x向右平移2个单位后与双曲线y=
如图,已知O为坐标原点,将直线y=x向右平移2个单位后与双曲线y=


 如图,在四边形ABCD中,∠A=∠BCD=90°,∠B=45°,
如图,在四边形ABCD中,∠A=∠BCD=90°,∠B=45°, 如图是一块蛋糕,表面的形状是平行四边形,且内有一个平行四边形的孔.你能一刀将它切成面积相等的两块吗?请说出你的切法,并画出示意图.
如图是一块蛋糕,表面的形状是平行四边形,且内有一个平行四边形的孔.你能一刀将它切成面积相等的两块吗?请说出你的切法,并画出示意图.