题目内容
1.因式分解:(1)x3-6x2y+9xy2-4y3
(2)x4+2x3y-3x2y2-4xy3+4y4.
分析 (1)三一分组、二二分组都不行,考虑拆项,把-4y3拆成-y3与x3组成立方差公式,剩余三项组,组后提取公因式;
(2)题目5项,考虑三二组合后再提取公因式.
解答 (1)x3-6x2y+9xy2-4y3
=x3-y3-6x2y+9xy2-3y3
=(x3-y3)-(6x2y-9xy2+3y3)
=(x-y)(x2+xy+y2)-3y(2x-y)(x-y)
=(x-y)(x2+xy+y2-6xy+3y2)
=(x-y)(x2-5xy+4y2)
=(x-y)(x-4y)(x-y)
=(x-y)2(x-4y)
(2)x4+2x3y-3x2y2-4xy3+4y4
=(x4+2x3y-3x2y2)-(4xy3-4y4)
=x2(x2+2xy-3y2)-4y3(x-y)
=x2(x+3y)(x-y)-4y3(x-y)
=(x-y)(x3+3x2y-4y3)
=(x-y)[(x3-y3)+(3x2y-3y3)]
=(x-y)[(x-y)(x2+xy+y2)+3y(x+y)(x-y)]
=(x-y)[(x-y)(x2+xy+y2+3xy+3y2)]
=(x-y)2(x2+4xy+4y2)
=(x-y)2(x+2y)2
点评 本题考查了因式分解的分组分解法,拆项恰当分组是关键.四项一般考虑一三或者二二分组,一三分组后运用平方差,二二分组后考虑提取公因式,五项,一般按按二三分组,分组后提取公因式.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
2.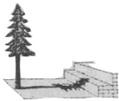 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )| A. | 6.93米 | B. | 8米 | C. | 11.8米 | D. | 12米 |
11.△ABC中,D是AB的中点,E是AC的三等分点(靠近A点),如果△ABC与△ADE相似,则相似比为( )
| A. | 2:3 | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | 1:$\sqrt{6}$ | D. | 4:9 |
 如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.
如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm. 已知如图,点F、A、E、B在一条直线上,∠C=∠F,BC∥DE,AB=DE
已知如图,点F、A、E、B在一条直线上,∠C=∠F,BC∥DE,AB=DE 如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,若CD=2cm,则AC=2+$2\sqrt{2}$(cm).
如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,若CD=2cm,则AC=2+$2\sqrt{2}$(cm). 如图,△ABC为等腰直角三角形,AE=AF,EH⊥BF,AM⊥BF,求证:HM=CM.
如图,△ABC为等腰直角三角形,AE=AF,EH⊥BF,AM⊥BF,求证:HM=CM. 如图为8×9的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上.
如图为8×9的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上.