题目内容
6.某商品售价为60元,每星期可卖出300件,市场调查反映,每降价1元,可多卖20件,进价为每件40元,若降价x元(x为整数)每星期利润为y元(1)求y与x的函敖关系;
(2)当售价为多少元时,每星期的利润最大;
(7)2015年2月份这种商品的利润超过24000元,问2015年2月份售价在什么范围(每星期售价保持下变).
分析 (1)根据题意表示出其销售量,根据每周利润=单件利润×每周销售量可列出函数关系式;
(2)将(1)中函数关系式配方成二次函数的顶点式可得最值情况;
(3)根据题意列出不等式,结合二次函数图象求出不等式的解集,即可得售价的范围.
解答 解:(1)设降价x元,则售价为(60-x)元,销售量为(300+20x)件,
根据题意得y=(60-x-40)(300+20x)=-20x2+100x+6000;
(2)∵y=-20x2+100x+6000=-20(x-2.5)2+6125,
∴当x=2.5时,即售价为60-2.5=57.5时,每星期利润最大,为6125元,
答:当售价为57.5元时,每星期的利润最大;
(3)根据题意,得:4(-20x2+100x+6000)>24000,
解得:0<x<5,
则售价55<60-x<60,
答:2015年2月份售价在55元至60元范围.
点评 本题主要考查二次函数的实际应用能力,理解题意准确抓住相等关系是列出函数关系式及解决以后问题的根本,利用二次函数的性质解决相关问题是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若a<b,则下列不等式的变形中不正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{5}$$<\frac{b}{5}$ | C. | 5a-1<5b-1 | D. | 5-a<5-b |
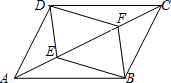 已知:如图,在四边形ABCD中,E、F是四边形ABCD的对角线AC上的两点,且AF=CE,DF=BE,DF∥BE.
已知:如图,在四边形ABCD中,E、F是四边形ABCD的对角线AC上的两点,且AF=CE,DF=BE,DF∥BE.