题目内容
17.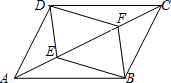 已知:如图,在四边形ABCD中,E、F是四边形ABCD的对角线AC上的两点,且AF=CE,DF=BE,DF∥BE.
已知:如图,在四边形ABCD中,E、F是四边形ABCD的对角线AC上的两点,且AF=CE,DF=BE,DF∥BE.(1)求证:△CDF≌△ABE;
(2)求证:四边形ABCD是平行四边形.
分析 (1)只要证明CF=AE,∠DFC=∠AEB,根据SAS即可判定.
(2)只要证明CD=AB,CD∥AB即可.
解答 (1)证明: ∵DF∥EB,
∵DF∥EB,
∴∠DFE=∠BEF,
∵∠DFC+∠DFE=180°,∠AEB+∠BEF=180°,
∴∠DFC=∠AEB,
∵AF=CE,
∴AE=CF,
在△FCD和△EAB中,
$\left\{\begin{array}{l}{DF=EB}\\{∠DFC=∠AEB}\\{FC=AE}\end{array}\right.$,
∴△FCD≌△EAB.
(2)∵△FCD≌△EAB,
∴CD=AB,∠DCF=∠BAE,
∴DC∥AB,又∵CD=AB,
∴四边形ABCD是平行四边形.
点评 本题考查全等三角形的判定和性质、平行四边形的判定等知识,解题的关键是寻找全等的条件,记住全等三角形的判定方法,平行四边形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
5.不等式3x+2>2x的解集是( )
| A. | x<-2 | B. | x<-1 | C. | x<0 | D. | x>-2 |




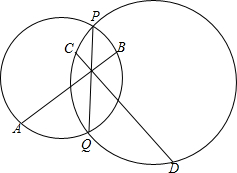 如图,PQ为两圆的公共弦,M为PQ上一点,AB、CD分别是两圆的弦且它们相交于M,求证:A、C、B、D四点共圆.
如图,PQ为两圆的公共弦,M为PQ上一点,AB、CD分别是两圆的弦且它们相交于M,求证:A、C、B、D四点共圆.