题目内容
14．阅读以下材料，解答问题：例：设y=x2-4x+2，求y的最值．
解：y=x2-4x+2=x2-2•2•x+22-2=（x-2）2-2
∵（x-2）2≥0
∴（x-2）2-2≥-2，即y有最小值是-2，
问题：（1）设y=x2-6x-1，求y的最值．
（2）设y=-x2+8x+1，求y的最值．
分析 （1）类比例题，将y=x2-6x-1配方成y=（x-3）2-10可知最值情况；
（2）将y=-x2+8x+1配方成y=-（x-4）2+17可知最值情况．
解答 解：（1）y=x2-6x-1=x2-2•3•x+32-10=（x-3）2-10，
∵（x-3）2≥0，
∴（x-3）2-10≥-10，即y有最小值-10；
（2）y=-x2+8x+1=-（x2-2•4•x+42-42）+1=-（x-4）2+17，
∵-（x-4）2≤0，
∴-（x-4）2+17≤17，即y有最大值17．
点评 本题主要考查配方法求函数最值的能力，熟悉完全平方公式是配方的根本和关键，要注意配上多少还要减去多少以保证等式仍然成立．
练习册系列答案
相关题目
4．
小亮和小明周六到距学校24km的滨湖湿地公园春游，小亮8：00从学校出发，骑自行车去湿地公园，小明8：30从学校出发，乘车沿相同路线去滨湖湿地公园，在同一直角坐标系中，小亮和小明的行进路程S（km）与时间t（时）的函数图象如图所示．根据图象得到结论，其中错误的是（ ）
小亮和小明周六到距学校24km的滨湖湿地公园春游，小亮8：00从学校出发，骑自行车去湿地公园，小明8：30从学校出发，乘车沿相同路线去滨湖湿地公园，在同一直角坐标系中，小亮和小明的行进路程S（km）与时间t（时）的函数图象如图所示．根据图象得到结论，其中错误的是（ ）| A． | 小亮骑自行车的平均速度是12km/h | |
| B． | 小明比小亮提前0.5小时到达滨湖湿地公园 | |
| C． | 小明在距学校12km处追上小亮 | |
| D． | 9：30小明与小亮相距4km |
5．不等式3x+2＞2x的解集是（ ）
| A． | x＜-2 | B． | x＜-1 | C． | x＜0 | D． | x＞-2 |
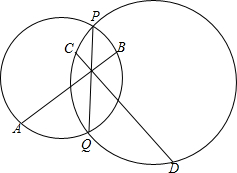如图，PQ为两圆的公共弦，M为PQ上一点，AB、CD分别是两圆的弦且它们相交于M，求证：A、C、B、D四点共圆．