题目内容
11.等腰三角形一腰上的高与底边的夹角为20°,则它的底角为70°,当腰上的高与底边的夹角为60°时,它的底角为30°,若等腰三角形一腰上的高与另一腰的夹角为50°,则它的底角为70°或20°.分析 已知一腰上的高与底边的夹角根据直角三角形两锐角互余求得∠C的度数,然后根据等腰三角形的性质即可求得;已知等腰三角形一腰上的高与另一腰的夹角,据直角三角形两锐角互余求得∠A的度数,然后分两种情况根据等腰三角形的性质求得即可.
解答 解:等腰三角形一腰上的高与底边的夹角为20°时,如图1,
∵△ABC是等腰三角形,BD⊥AC,∠CDB=90°,∠CBD=20°,
∴在直角△BDC中,∠C=90°-20°=70°,
∴∠C=∠ABC=70°;
当腰上的高与底边的夹角为60°时,如图2,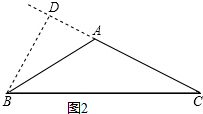
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠CBD=60°,
∴在直角△CBD中,∠C=90°-60°=30°,
∴∠C=∠ABC=30°.
当等腰三角形一腰上的高与另一腰的夹角为50°时,分两种情况:
①如图1,∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠A=90°-50°=40°,
∴∠C=∠ABC=$\frac{180°-40°}{2}$=70°;
②如图2,∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠BAD=90°-50°=40°,
又∵∠BAD=∠ABC+∠C,∠ABC=∠C,
∴∠C=∠ABC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×40°=20°.
故答案为:70°;30°;70°或20°.
点评 本题主要考查了等腰三角形的性质,直角三角形的性质,三角形内角和定理,分类讨论思想的运用是解答本题的关键.

练习册系列答案
相关题目
19.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,则代数式x02-(x1+x2)x0+x1x2的值( )
| A. | 等于0 | B. | 恒正 | C. | 恒负 | D. | 不能确定 |
3.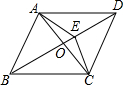 如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
 如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )| A. | 点E是△ACD的内心 | B. | ∠DBC=35° | C. | CE=DE | D. | △ABO≌△CBO |
 如图,已知a∥b,∠1=135°,则∠2=45°.
如图,已知a∥b,∠1=135°,则∠2=45°.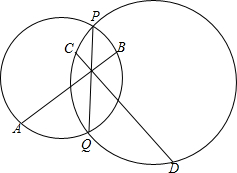 如图,PQ为两圆的公共弦,M为PQ上一点,AB、CD分别是两圆的弦且它们相交于M,求证:A、C、B、D四点共圆.
如图,PQ为两圆的公共弦,M为PQ上一点,AB、CD分别是两圆的弦且它们相交于M,求证:A、C、B、D四点共圆.