题目内容
18.若a、b为方程x2-4(x+1)=1的两根,则$\frac{a}{b}$=-5或-$\frac{1}{5}$.分析 首先把原方程整理为x2-4x-5=0,再利用因式分解法求出方程的两根,进而求出$\frac{a}{b}$的值.
解答 解:∵x2-4(x+1)=1,
∴x2-4x-5=0,
∴(x-5)(x+1)=0,
∴x-5=0或x+1=0,
∴x1=5,x2=-1,
∴$\frac{a}{b}$=-5或-$\frac{1}{5}$,
故答案为-5或-$\frac{1}{5}$.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
6.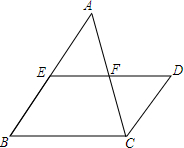 如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )
如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )
 如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )
如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )| A. | 相等 | B. | 平行 | C. | 平行且相等 | D. | 以上都不是 |
7.已知a和b一正一负,则$\frac{|a|}{a}$+$\frac{|b|}{b}$的值为( )
| A. | 0 | B. | 2 | C. | -2 | D. | 根据a、b的值确定 |
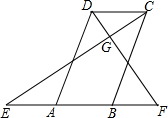 已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.
已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.
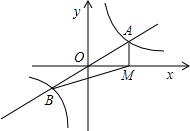 如图,直线y=mx与双曲线$y=\frac{k}{x}$交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若S△ABM=4,则k的值是( )
如图,直线y=mx与双曲线$y=\frac{k}{x}$交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若S△ABM=4,则k的值是( )