题目内容
8.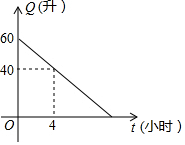 汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图所示,当油箱中余油20升时,该汽车行驶了8小时.
汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图所示,当油箱中余油20升时,该汽车行驶了8小时.
分析 设一次函数的表达式为Q=kt+b(k≠0),然后利用待定系数法求一次函数解析式,把余油量代入函数解析式求出时间t即可.
解答 解:设一次函数的表达式为Q=kt+b(k≠0)
由图象可知,函数图象过(0,60)和(4,40)两点,
∴$\left\{\begin{array}{l}{b=60}\\{4k+b=40}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-5}\\{b=60}\end{array}\right.$,
∴Q=-5t+60;
当Q=20时,-5t+60=20,
解得t=8,
∴当油箱中余油20升时,该汽车行驶了8小时.
故答案为8.
点评 此题考查了一次函数的应用,已知函数值求自变量的方法,利用待定系数法求出一次函数解析式是解题的关键,也是本题的难点

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
16.对于函数y=-$\frac{3}{x}$,当x<0时,函数图象位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列运算中错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2 $\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{(\sqrt{2}-\sqrt{3})^{2}}$=$\sqrt{2}-\sqrt{3}$ |
18.在下列给出的各数中,最小的一个是( )
| A. | -2 | B. | $-\sqrt{5}$ | C. | 0 | D. | 1 |
 设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.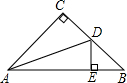 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.