题目内容
19.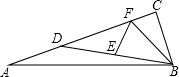 如图,在△ABC中,∠C=90°,点D在AC上,AD=BC=2,E是BD中点,点F在线段CD上,∠DFE=45°,DF=3,求EF、AB的长.
如图,在△ABC中,∠C=90°,点D在AC上,AD=BC=2,E是BD中点,点F在线段CD上,∠DFE=45°,DF=3,求EF、AB的长.
分析 过点E作EM⊥CD于点M,由三角形的中位线结合BC的长度可得出EM的长度,结合∠DFE=45°即可得出△MEF为等腰直角三角形,由此即可得出MF、EF的长度,结合CF=3以及线段间的关系即可得出CD的长度,再根据AD=2利用勾股定理即可求出AB的长度.
解答 解:过点E作EM⊥CD于点M,如图所示.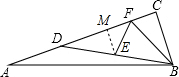
∵∠C=90°,点E为线段BD的中点,
∴EM∥BC,点M为线段CD的中点,EM为△DBC的中位线.
∵BC=2,
∴ME=$\frac{1}{2}$BC=1.
∵∠DFE=45°,
∴△MEF为等腰直角三角形,
∴MF=EM=1,EF=$\sqrt{2}$EM=$\sqrt{2}$.
∵DF=3,
∴DM=DF-MF=2,CD=2DM=4.
∵AD=BC=2,
∴AC=AD+CD=6.
在Rt△ABC中,BC=2,AC=6,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{10}$.
点评 本题考查了勾股定理、三角形的中位线以及等腰直角三角形的判定与性质,解题的关键是根据三角形的中位线求出EF、CD的长度.本题属于中档题,难度不大,解决该题型题目时,选用合适的辅助线是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.学校图书馆每天借出图书在50册左右,如果某天借出53册,就记作+3,如果某天借出40册,就记作-10,上星期借出图书记录如表:
上星期五星期二多借出15册;上星期平均每天借出51册.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 记录数值 | 0 | -7 | +6 | -2 | +8 |
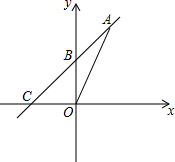 如图,一次函数y=kx+b的图象经过点A(2,4),B(0,2),与x轴交于点C,求三角形AOC的面积.
如图,一次函数y=kx+b的图象经过点A(2,4),B(0,2),与x轴交于点C,求三角形AOC的面积.