题目内容
11.如图1,关于x的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;
(3)如图2,F(3,0)为x轴上一点,直线l经过点F,在l上存在点M,使以AB为斜边的Rt△AMB只有一个,求直线l的方程.
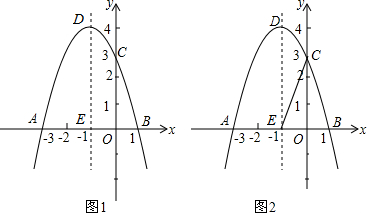
分析 (1)把A(-3,0),点C(0,3)代入y=-x2+bx+c解方程组即可.
(2)存在.如图1中,作PM⊥AD于M,设PM=PE=x,在Rt△PDM中,∵DM2+PM2=PD2,列出方程即可解决问题.
(3)如图3中,设AB为直径的⊙E交y轴于M、M′.连接EM,FM,FM′,AM,BM.首先证明直线FM、FM′就是满足条件的直线l,利用待定系数法即可解决问题.
解答 解:(1)∵二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),
∴$\left\{\begin{array}{l}{c=3}\\{-9-3b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2-2x+3.
(2)存在.
理由:如图1中,作PM⊥AD于M,设PM=PE=x,
∵AM=$\sqrt{A{P}^{2}-P{M}^{2}}$,AE=$\sqrt{A{P}^{2}-P{E}^{2}}$,
∴AM=AE=2,
∵AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=2$\sqrt{5}$,
∴DM=2$\sqrt{5}$-2,
在Rt△PDM中,∵DM2+PM2=PD2,
∴(2$\sqrt{5}$-2)2+x2=(4-x)2,
∴x=$\sqrt{5}$-1,
∴点P坐标(-1,$\sqrt{5}$-1).
(3)如图3中,设AB为直径的⊙E交y轴于M、M′.连接EM,FM,FM′,AM,BM.
∵EM=2,OE=1,
∴OM=$\sqrt{E{M}^{2}-E{O}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴FM=$\sqrt{O{M}^{2}+O{F}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{3}^{2}}$=2$\sqrt{3}$,
∵EM2+FM2=22+(2$\sqrt{3}$)2=16,EF2=42=16,
∴EF2=EM2+FM2,
∴∠EMF=90°,
∴FM是⊙E的切线,
∵AB是直径,
∴∠AMB=90°,
∴△ABM是直角三角形,
又直线FM与⊙E相切,
∴直线AM上存在点M,使以AB为斜边的Rt△AMB只有一个,同理直线FM′也是满足条件的直线l,
∴满足条件的直线l为y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$或y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$.
点评 本题考查二次函数综合题、待定系数法、勾股定理、圆、切线的判定等知识,解题的关键是熟练应用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,第三个问题想到直径所对的圆周角是直角解决问题,属于中考压轴题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案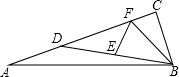 如图,在△ABC中,∠C=90°,点D在AC上,AD=BC=2,E是BD中点,点F在线段CD上,∠DFE=45°,DF=3,求EF、AB的长.
如图,在△ABC中,∠C=90°,点D在AC上,AD=BC=2,E是BD中点,点F在线段CD上,∠DFE=45°,DF=3,求EF、AB的长.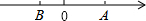 如图,点A,B在数轴上分别表示有理数m,n.求|m|+|n|的值.
如图,点A,B在数轴上分别表示有理数m,n.求|m|+|n|的值. 如图,某山坡的坡面AB=200m,坡角∠BAC=40°,则该山坡的高BC约为129m(用科学计算器计算,使结果精确到1).
如图,某山坡的坡面AB=200m,坡角∠BAC=40°,则该山坡的高BC约为129m(用科学计算器计算,使结果精确到1).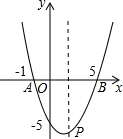 如图,抛物线经过A.B、C三点,求它的解析式和顶点P的坐标.
如图,抛物线经过A.B、C三点,求它的解析式和顶点P的坐标.