题目内容
16.画出函数y=x2-4的图象.(1)求抛物线与x轴的交点坐标.
(2)当x为何值时,y>0?y<0呢?
分析 画出图象即可求出抛物线与x轴的交点坐标以及y>0(<0)时的解集
解答  解:(1)函数y=x2-4的图象如图所示,
解:(1)函数y=x2-4的图象如图所示,
∴抛物线与x轴的交点坐标为(-2,0)、(2,0);
(2)当y>0时,
由图象可知:x<-2或x>2;
当y<0时,
由图象可知:-2<x<2;
点评 本题考查二次函数的图象,解题的关键是画出图象,然后根据图象写出x轴的交点坐标以及y>0时的解集,本题属于基础题型.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
19.为了推进我州校园篮球运动的发展,2017年四川省中小学生男子篮球赛于2月在西昌成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:
(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
| 篮球 | 排球 | |
| 进价(元/个) | 80 | 50 |
| 售价(元/个) | 105 | 70 |
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
20. 把一块等腰直角三角尺和直尺如图放置,如果∠1=30°,则∠2的度数为( )
把一块等腰直角三角尺和直尺如图放置,如果∠1=30°,则∠2的度数为( )
 把一块等腰直角三角尺和直尺如图放置,如果∠1=30°,则∠2的度数为( )
把一块等腰直角三角尺和直尺如图放置,如果∠1=30°,则∠2的度数为( )| A. | 45° | B. | 30° | C. | 20° | D. | 15° |
5.已知抛物线y=ax2+bx+c(a<0)过A(-4,1),B(0,1),C(x1,y1),D(x2,y2)四点,且y1<y2,则x1与x2的取值可能是( )
| A. | x1=-1,x2=1 | B. | x1=-5,x2=1 | C. | x1=3,x2=-3 | D. | x1=1,x2=-6 |
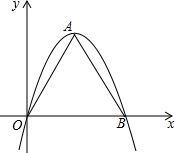 如图一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”
如图一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”