题目内容
12. 如图,在△ABC中,∠B=22.5°,∠C=60°,AB的垂直平分线交BC于点D,BD2=72,AE⊥BC于E,求EC2的值.
如图,在△ABC中,∠B=22.5°,∠C=60°,AB的垂直平分线交BC于点D,BD2=72,AE⊥BC于E,求EC2的值.
分析 首先作出辅助线连接AD,再利用线段垂直平分线的性质计算.
解答  解:连接AD,
解:连接AD,
已知DF垂直且平分AB⇒BD=AD,
∵∠B=22.5°,∠C=60°,
∴∠BAC=97.5°,
根据三角形外角与外角性质可得,
∠ADE=∠B+∠DAB=45°,AE⊥BC,
∴∠DAE=45°,
∴△AED为等腰三角形,
根据等腰三角形的性质可得DE=AE=6,
∵∠C=60°,
∴∠CAE=90°-60°=30°,
∴AC=2CE,
在Rt△ACE中,AC2=AE2+CE2,
即4CE2=62+CE2,
∴CE2=12.
点评 本题考查了线段垂直平分线的性质,三角形的外角的性质,等腰三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
4.方程x2-5=0的解是( )
| A. | x1=x2=5 | B. | x1=x2=-$\sqrt{5}$ | C. | x1=$\sqrt{5}$,x2=-$\sqrt{5}$ | D. | x=$\sqrt{5}$ |
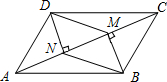 已知AC是平行四边形ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足分别是M,N,求证:DM∥BN.
已知AC是平行四边形ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足分别是M,N,求证:DM∥BN. 如图,一个矩形花园的长为15m,宽为10m,在中间开出等宽的两条观赏道,结果花园的面积减少了16%,则观赏道的宽为1m.
如图,一个矩形花园的长为15m,宽为10m,在中间开出等宽的两条观赏道,结果花园的面积减少了16%,则观赏道的宽为1m.