题目内容
7.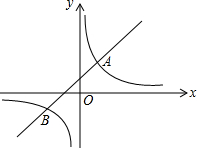 如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.
如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.
分析 先把B点坐标代入y=$\frac{{k}_{2}}{x}$求出k2=2,得到双曲线的解析式为y=$\frac{2}{x}$,再把A(m,2)代入y=$\frac{2}{x}$确定A点坐标,然后观察函数图象得到当x>1或-2<x<0时,一次函数图象都在反比例函数图象上方,即k1x+b>$\frac{{k}_{2}}{x}$.
解答 解:∵双曲线y=$\frac{{k}_{2}}{x}$经过点B(-2,-1),
∴k2=2,
∴双曲线的解析式为y=$\frac{2}{x}$;
∵点A(m,2)在双曲线y=$\frac{2}{x}$上,
∴2=$\frac{2}{m}$,解得m=1,
∴A点坐标为(1,2),
由图可知x>1或-2<x<0.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.不等式组$\left\{\begin{array}{l}{x-1≤0}\\{6-3x>0}\end{array}\right.$的解集为( )
| A. | x≤1 | B. | x>-2 | C. | -2≤x≤1 | D. | 无解 |
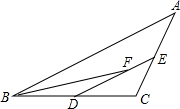 在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )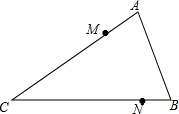 如图,在∠ACB内部求作一个点P,使PM=PN,且点P到CA、CB的距离相等.(尺规作图,不写作法,保留作图痕迹)
如图,在∠ACB内部求作一个点P,使PM=PN,且点P到CA、CB的距离相等.(尺规作图,不写作法,保留作图痕迹)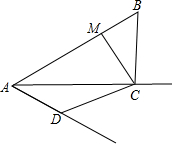 如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
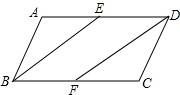 如图,在?ABCD中,点E、F分别在边AD,BC上,且BE∥DF.若∠EBF=50°,则∠EDF的度数是50°.
如图,在?ABCD中,点E、F分别在边AD,BC上,且BE∥DF.若∠EBF=50°,则∠EDF的度数是50°.