题目内容
8.$\frac{3a}{5xy}$=$\frac{()}{10axy}$,(a≠0);$\frac{a+2}{{a}^{2}-4}$=$\frac{1}{()}$;③$\frac{-2x}{1-2x}$=$\frac{()}{2{x}^{2}-x}$.分析 根据分式的基本性质,找出分子或分母同乘或除的式子即可.
解答 解:$\frac{3a}{5xy}$=$\frac{()}{10axy}$,分母乘2a,则分子乘2a为6a2;
$\frac{a+2}{{a}^{2}-4}$=$\frac{1}{()}$,分子除a+2,则分母除a+2为a-2;
$\frac{-2x}{1-2x}$=$\frac{()}{2{x}^{2}-x}$,分母乘-x,则分子乘-x为2x2.
故答案为:6a2;a-2;2x2.
点评 本题考查了分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变;分子、分母、分式本身同时改变两处的符号,分式的值不变.

练习册系列答案
相关题目
18.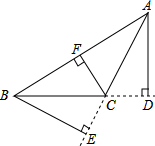 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )| A. | CF | B. | BE | C. | AD | D. | CD |
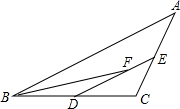 在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )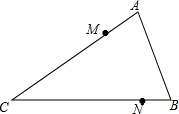 如图,在∠ACB内部求作一个点P,使PM=PN,且点P到CA、CB的距离相等.(尺规作图,不写作法,保留作图痕迹)
如图,在∠ACB内部求作一个点P,使PM=PN,且点P到CA、CB的距离相等.(尺规作图,不写作法,保留作图痕迹)