题目内容
19. 如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AC的长为( )
如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AC的长为( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
分析 首先连接AO并延长,交CD于点E,连接OC,由直线AB与⊙O相切于点A,根据切线的性质,可得AE⊥AB,又由CD∥AB,可得AE⊥CD,然后由垂径定理与勾股定理,求得OE的长,继而求得AC的长.
解答 解:连接AO并延长,交CD于点E,连接OC,
∵直线AB与⊙O相切于点A,
∴EA⊥AB,
∵CD∥AB,
∠CEA=90°,
∴AE⊥CD,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$×4=2,
∵在Rt△OCE中,OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\frac{3}{2}$,
∴AE=OA+OE=4,
∴在Rt△ACE中,AC=$\sqrt{C{E}^{2}+A{E}^{2}}$=2$\sqrt{5}$.
故选A.
点评 此题考查了切线的性质、垂径定理、勾股定理以及平行线的性质.此题难度适中,正确的添加辅助线是解题的关键.

练习册系列答案
相关题目
10.n边形的内角和与外角和相等,则n=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.已知等腰三角形的一个内角为65°,则其顶角为( )
| A. | 50° | B. | 65° | C. | 115° | D. | 50°或65° |
14. 如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
 如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )| A. | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | B. | a+b<0 | C. | |a+b|-a=b | D. | -b<a<-a<b |
8. 如图,能用图中字母表示出来的不同射线共有( )
如图,能用图中字母表示出来的不同射线共有( )
 如图,能用图中字母表示出来的不同射线共有( )
如图,能用图中字母表示出来的不同射线共有( )| A. | 3条 | B. | 4条 | C. | 6条 | D. | 8条 |
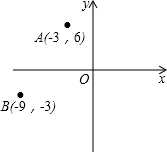 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是(-1,2)或(1,-2).
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是(-1,2)或(1,-2). 如图,已知线段AB=8cm,延长线段AB到C,使BC=2AB,点D是AC的中点,则BD等于4cm.
如图,已知线段AB=8cm,延长线段AB到C,使BC=2AB,点D是AC的中点,则BD等于4cm. 阳光下,小亮测量“望月阁”的高AB.(如图),由于观测点与“望月阁”底部间的距离不易测得,因此他首先在直线BM上点C处固定平放一平面镜,在镜面上做了一个标记,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
阳光下,小亮测量“望月阁”的高AB.(如图),由于观测点与“望月阁”底部间的距离不易测得,因此他首先在直线BM上点C处固定平放一平面镜,在镜面上做了一个标记,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.