题目内容
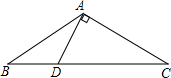 如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.
如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.考点:含30度角的直角三角形,等腰三角形的判定与性质
专题:
分析:根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°,∠BAC=120°,求出∠B=∠BAD,推出AD=BD,根据含30度角的直角三角形性质求出CD=2AD=2BD,即可得出答案.
解答:解:∵在△ABC中,AB=AC,∠C=30°,
∴∠B=∠C=30°,∠BAC=180°-30°-30°=120°,
∵DA⊥AC,
∴∠DAC=90°,
∴∠BAD=120°-90°=30°,
∴∠B=∠BAD,
∴BD=AD,
∵∠DAC=90°,∠C=30°,
∴CD=2AD,
∴CD=2BD,
∵BC=BD+CD=6cm,
∴BD=2cm.
∴∠B=∠C=30°,∠BAC=180°-30°-30°=120°,
∵DA⊥AC,
∴∠DAC=90°,
∴∠BAD=120°-90°=30°,
∴∠B=∠BAD,
∴BD=AD,
∵∠DAC=90°,∠C=30°,
∴CD=2AD,
∴CD=2BD,
∵BC=BD+CD=6cm,
∴BD=2cm.
点评:本题考查了等腰三角形的性质,含30度角的直角三角形性质的应用,解此题的关键是求出CD=2BD,题目比较典型,难度适中.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
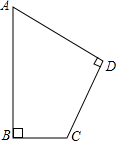 某片绿地的形状为四边形ABCD(如图),其中∠A=60°,AB⊥BC,AB=200m,CD=100m,求绿地周长(精确到1m)
某片绿地的形状为四边形ABCD(如图),其中∠A=60°,AB⊥BC,AB=200m,CD=100m,求绿地周长(精确到1m) 如图,根据图中所给的数据,求四边形ABCD的面积.
如图,根据图中所给的数据,求四边形ABCD的面积.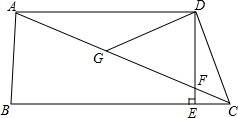 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.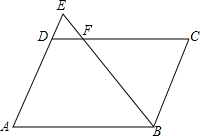 平行四边形ABCD的面积是30cm2,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大9cm2,且AD=5cm,那么DE等于多少cm?
平行四边形ABCD的面积是30cm2,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大9cm2,且AD=5cm,那么DE等于多少cm? 如图,点C在线段AB上,点M、N分别是AC,BC的中点.
如图,点C在线段AB上,点M、N分别是AC,BC的中点.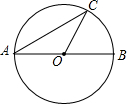 如图,已知在⊙O中,AB是直径,C为⊙O上一点,若AB=5,∠BOC=60°,求AC的长.
如图,已知在⊙O中,AB是直径,C为⊙O上一点,若AB=5,∠BOC=60°,求AC的长.
 如图,BE平分∠ABC,且∠1=∠3,则DE与BC平行吗?为什么?
如图,BE平分∠ABC,且∠1=∠3,则DE与BC平行吗?为什么?