题目内容
19．下列说法正确的是（ ）| A． | 所有的等腰三角形都相似 | B． | 有一对锐角相等的两个三角形相似 | ||
| C． | 相似三角形都是全等的 | D． | 所有的等边三角形都相似 |
分析 根据相似图形的判定定理对四个选项进行逐一判断即可．
解答 解：A、等腰三角形的底角与顶角均不能确定，边长也不确定，故本选项错误；
B、有一对锐角相等的两个直角三角形相似，故本选项错误；
C、全等三角形只是一种特殊的相似三角形，所以相似三角形不一定是全等的，故本选项错误；
D、由于所有的等边三角形的各角是60°，而每个等边三角形的边长相等，故所有的等边三角形都相似，故本选项正确；
故选：D．
点评 本题考查的是相似图形，熟知等腰三角形、等边三角形以及锐角三角形性质是解答此题的关键．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
如图，在△ABC中，BD、CE是高，G、F分别是BC、DE的中点，连接GF，求证：GF⊥DE．
如图，点F、C在BE上，AB∥DE，∠A=∠D，BF=CE，求证：AB=DE．
7．用配方法解方程2x2+3x-1=0，则方程可变形为（ ）
| A． | （x+3）2=$\frac{1}{3}$ | B． | （x+$\frac{3}{4}$）2=$\frac{1}{2}$ | C． | （3x+1）2=1 | D． | （x+$\frac{3}{4}$）2=$\frac{17}{16}$ |
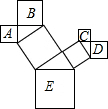如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、4、2、3，则最大正方形E的面积是38．