题目内容
11.某校70周年校庆将于本周六举行,为了迎接校友的到来,学生会的同学们用红色和白色的康乃馨花自制了A、B两种样式的手捧花.其中制作A样式手捧花一束分别用康乃馨红色1支,白色7支;
其中制作B样式手捧花一束分别用康乃馨红色3支,白色5支;
(1)要制作100束手捧花,现有红色康乃馨201支,求百色康乃馨至少要多少支?
(2)现制作过程中恰好用红色康乃馨200支,白色康乃馨a支,其中724<a<758
①求此时制作A、B两种样式的手捧花各多少束?
②请直接写出满足条件的a的值738或745.
分析 (1)设A样式手捧花x束,则B样式手捧花(100-x)束,根据现有红色康乃201支列出不等式,当x有最小值时,白色康乃馨最少,由此解答即可;
(2)设A样式手捧花用红色康乃馨x支,则B样式手捧花用红色康乃馨200-x支,共需要白色康乃馨a=7x+5×$\frac{200-x}{3}$代入不等式建立不等式组求得答案即可.
解答 解:(1)设A样式手捧花x束,则B样式手捧花(100-x)束,由题意得
x+3(100-x)≤201,
解得:x≥49.5.
则x最小为50,所以A,B两种样式的手捧花至少50束,白色康乃馨最少7×50+5×50=600支;
(2)①设A样式手捧花用红色康乃馨x支,则B样式手捧花用红色康乃馨200-x支,由题意得
$\left\{\begin{array}{l}{7x+5×\frac{200-x}{3}>724}\\{7x+5×\frac{200-x}{3}<758}\end{array}\right.$,
解得:73.25<x<79.625,
则x=74,75,76,77,78,79,
则$\frac{200-x}{3}$是整数的有x=74,77,
对应a=728,744,
当x=74,200-x=126,制作A种样式的手捧花74束,制作B种样式的手捧花42束;
当x=77,200-x=123,制作A种样式的手捧花77束,制作B种样式的手捧花41束.
②当x=74或77时,a=7x+5×$\frac{200-x}{3}$=728或744.
点评 此题考查一元一次不等式组的实际运用,找出题目蕴含的数量关系和不等关系是解决问题的关键.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 所有的等腰三角形都相似 | B. | 有一对锐角相等的两个三角形相似 | ||
| C. | 相似三角形都是全等的 | D. | 所有的等边三角形都相似 |
 已知:如图,△ABC中.
已知:如图,△ABC中.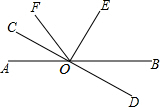 如图,已知直线AB和CD都交于点O,∠COE=90°,且OF平分∠AOE.
如图,已知直线AB和CD都交于点O,∠COE=90°,且OF平分∠AOE.
 如图,在平行四边形ABCD中,AB=5cm,Bc=8cm,∠BAD=120°,CE⊥AB于E,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,AB=5cm,Bc=8cm,∠BAD=120°,CE⊥AB于E,求平行四边形ABCD的面积.