题目内容
4.在平面直角坐标系中,点A(-3,0),B(4,0),C(0,3),∠ABC的角平分线BD交AC于D,点P在射线BD上移动,点E在x轴上移动.若BC=5,则PA+PE的最小值是$\frac{21}{5}$.分析 延长BC到A′,使BA′=BA,则点A′是点A关于直线BD的对称点,于是得到BA′=BA=7,连接A′E,交射线BD于P,则P就是使PA+PE的最小值的点,它的位置随点E的移动而变化,根据“垂线段最短”得:当A′E⊥x轴时,A′E最短,即PA+PE最小,通过△BOC∽△BA′E′,列比例式即可得到结论.
解答 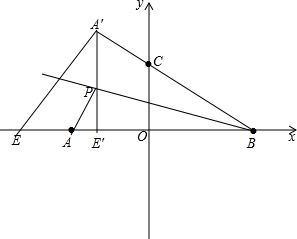 解:延长BC到A′,使BA′=BA,
解:延长BC到A′,使BA′=BA,
∵∠ABC的角平分线BD交AC于D,
∴点A′是点A关于直线BD的对称点,
∴BA′=BA=7,
连接A′E,交射线BD于P,
则P就是使PA+PE的最小值的点,
它的位置随点E的移动而变化,
且PA+PE=A′E,
根据“垂线段最短”得:当A′E⊥x轴时,A′E最短,即PA+PE最小,
∵A′E′⊥x轴,OC⊥x轴,
∴OC∥A′E′,
∴△BOC∽△BA′E′,
∴$\frac{A′E′}{OC}=\frac{A′B}{BC}$,
即$\frac{A′E′}{3}=\frac{7}{5}$,
∴A′E′=$\frac{21}{5}$,即PA+PE的最小值=$\frac{21}{5}$.
故答案为:$\frac{21}{5}$.
点评 此题主要考查轴对称--最短路线问题,坐标与图形的性质,相似三角形的判定和性质,正确的作出图形是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.若x与y互为相反数,a与b互为倒数,则代数式$\frac{1}{2}$(x+y)+3ab的值为( )
| A. | 0 | B. | 1 | C. | 3 | D. | 无法计算 |
19.下列说法正确的是( )
| A. | 所有的等腰三角形都相似 | B. | 有一对锐角相等的两个三角形相似 | ||
| C. | 相似三角形都是全等的 | D. | 所有的等边三角形都相似 |
 如图所示,按要求作出下列图形:
如图所示,按要求作出下列图形: