题目内容
14.在Rt△ABC中,∠ACB=90°,∠A=2∠B.(1)求sinB+tanA-6tanB+$\sqrt{3}$sinA的值;
(2)如果AB=8,求△ABC的周长.
分析 (1)根据三角形的内角和得到∠A+∠B=90°,由已知条件得到∠A=60°,∠B=30°,代入代数式即可得到结论;
(2)在Rt△ABC中,根据三角函数求得AC=4,BC=4$\sqrt{3}$,于是得到结论.
解答 解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=2∠B,
∴∠A+∠B=90°,
∴∠A=60°,∠B=30°,
∴sinB+tanA-6tanB+$\sqrt{3}$sinA=$\frac{1}{2}$$+\sqrt{3}$-6×$\frac{\sqrt{3}}{3}$+$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=2-$\sqrt{3}$;
(2)∵AB=8,
∴AC=AB•sinB=8×sin30°=4,BC=AB•cosB=8×cos30°=4$\sqrt{3}$,
∴△ABC的周长=AB+BC+AC=8+4+4$\sqrt{3}$=12+4$\sqrt{3}$.
点评 本题考查了解直角三角形,求特殊角的三角函数,熟练掌握直角三角形的边角关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.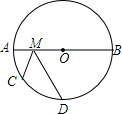 如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
 如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )| A. | 8 | B. | 6 | C. | 2+2$\sqrt{7}$ | D. | 4$\sqrt{3}$ |
9.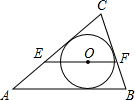 如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
 如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )| A. | EF>AE+BF | B. | EF<AE+BF | C. | EF2=AE•BF | D. | EF=AE+BF |
19.下列说法正确的是( )
| A. | 所有的等腰三角形都相似 | B. | 有一对锐角相等的两个三角形相似 | ||
| C. | 相似三角形都是全等的 | D. | 所有的等边三角形都相似 |
4.下列数中,是负数的是( )
| A. | |-2| | B. | (-1)2 | C. | 0 | D. | -3 |
 已知:如图,∠B=∠C=90°,AF=DE,BE=CF.
已知:如图,∠B=∠C=90°,AF=DE,BE=CF.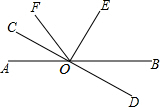 如图,已知直线AB和CD都交于点O,∠COE=90°,且OF平分∠AOE.
如图,已知直线AB和CD都交于点O,∠COE=90°,且OF平分∠AOE.