题目内容
13.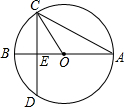 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$ | D. | 4 |
分析 利用垂径定理得CE=DE,再利用用圆周角定理∠BOC=45°,易得OE=OC,利用勾股定理可得CE,得CD.
解答 解:∵直径AB垂直于弦CD,
∴CE=DE=$\frac{1}{2}$CD,
∵∠A=22.5°,
∴∠BOC=45°,
∴OE=CE,
设OE=CE=x,
∵OC=2,
∴x2+x2=4,
解得:x=$\sqrt{2}$,
即:CE=2,
∴CD=2$\sqrt{2}$,
故选A.
点评 本题主要考查了垂径定理和圆周角定理,利用方程思想和勾股定理是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5. 如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )
 如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )| A. | 17° | B. | 34° | C. | 56° | D. | 124° |
2.甲、乙、丙三位选手在相同条件下各射击10次,射击成绩的平均数和方差如下表:
则射击成绩最稳定的选手是乙(填“甲”“乙”或“丙”).
| 选手 | 甲 | 乙 | 丙 |
| 平均数 | 9.3 | 9.3 | 9.3 |
| 方差 | 0.026 | 0.015 | 0.032 |
3.下列计算正确的是( )
| A. | (a3)2=a5 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-8}$=-2 | D. | a6÷a2=a3 |
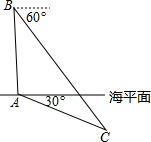 中国与俄罗斯两国海军正在黑海进行联合演习,在演习中我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1600米的反潜直升机B测得潜艇C的俯角为60°,试根据以上数据求出潜艇C离海平面的下潜深度.
中国与俄罗斯两国海军正在黑海进行联合演习,在演习中我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1600米的反潜直升机B测得潜艇C的俯角为60°,试根据以上数据求出潜艇C离海平面的下潜深度.