题目内容
3.在一只不透明的纸盒中装有2颗白旗子和3颗黑棋子,这些棋子除颜色外都相同.若在这只盒中再放入x颗黑棋子,搅匀后,已知从中任意摸出一颗棋子是白棋子的概率是$\frac{1}{4}$,则x=3.分析 根据纸盒中装有2颗白棋子和3颗黑棋子,再放入x颗黑棋子,故棋子的总数为2+3+x,再根据从中任意摸出一颗棋子是白棋子的概率是$\frac{1}{4}$,列式解答即可.
解答 解:∵在一只不透明的纸盒中装有2颗白棋子和3颗黑棋子,这些棋子除颜色外都相同.若在这只盒中再放入x颗黑棋子,
∴棋子的总数为2+3+x,
∵搅匀后,已知从中任意摸出一颗棋子是白棋子的概率是$\frac{1}{4}$,
∴$\frac{2}{2+3+x}$=$\frac{1}{4}$,
解得x=3.
故答案为3.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
13.|-2+3×(-2)|=( )
| A. | -8 | B. | 2 | C. | 4 | D. | 8 |
18.计算:
(1)$\sqrt{4}$-(3-$\sqrt{2}$)0+($\frac{1}{3}$)-2;
(2)(a-$\frac{1}{a}$)+$\frac{{a}^{2}-2a+1}{a}$.
(1)$\sqrt{4}$-(3-$\sqrt{2}$)0+($\frac{1}{3}$)-2;
(2)(a-$\frac{1}{a}$)+$\frac{{a}^{2}-2a+1}{a}$.
8.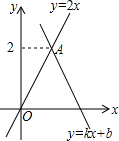 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
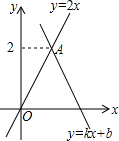 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | x>0 | B. | 0<x<1 | C. | 1<x<2 | D. | x>2 |
13.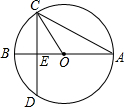 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$ | D. | 4 |
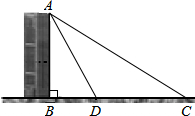 如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.
如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.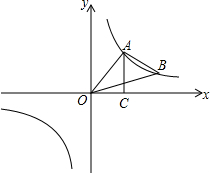 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且点A,B的横坐标分别为a和2a(a>0).过点A作x轴的垂线,垂足为C,连接OA,△AOC的面积为2.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且点A,B的横坐标分别为a和2a(a>0).过点A作x轴的垂线,垂足为C,连接OA,△AOC的面积为2.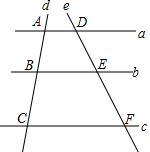 如图,已知直线a∥b∥c,直线d分别于直线a、b、c相交于点A、B、C,直线e分别与直线a、b、c相交于点D、E、F.若AB=2,BC=3,DE=3,则DF的长为$\frac{15}{2}$.
如图,已知直线a∥b∥c,直线d分别于直线a、b、c相交于点A、B、C,直线e分别与直线a、b、c相交于点D、E、F.若AB=2,BC=3,DE=3,则DF的长为$\frac{15}{2}$.