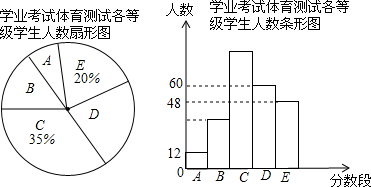
题目内容
18.观察下列等式:第一个等式:a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$
第二个等式:a2=$\frac{4}{2×3×{2}^{3}}=\frac{1}{2×{2}^{2}}-\frac{1}{3×{2}^{3}}$
第三个等式:a3=$\frac{5}{3×4×{2}^{4}}=\frac{1}{3×{2}^{3}}-\frac{1}{4×{2}^{4}}$
第四个等式:a4=$\frac{6}{4×5×{2}^{5}}=\frac{1}{4×{2}^{4}}-\frac{1}{5×{2}^{5}}$
按上述规律,回答以下问题:
(1)用含n的代数式表示第n个等式:an=$\frac{n+2}{n(n+1){•2}^{n+1}}$=$\frac{1}{n{•2}^{n}}-\frac{1}{(n+1){•2}^{n+1}}$;
(2)式子a1+a2+a3+…a2014=$\frac{1}{2}-\frac{1}{2015{×2}^{2015}}$.
分析 (1)首先根据前四个等式的特征,可得第n个等式的分子是n+2,分母是n(n+1)•2n+1;然后判断出后面算式的两个数的分子都是1,第一个数的分母是n•2n,第二个数的分母是(n+1)•2n+1,据此解答即可.
(2)根据题意,把前2014个等式左右两边分别相加,求出a1+a2+a3+…a2014的值是多少即可.
解答 解:(1)根据分析,可得
用含n的代数式表示第n个等式:an=$\frac{n+2}{n(n+1){•2}^{n+1}}$=$\frac{1}{n{•2}^{n}}-\frac{1}{(n+1){•2}^{n+1}}$;
(2)a1+a2+a3+…a2014
=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$+$\frac{1}{2{×2}^{2}}$-$\frac{1}{3{×2}^{3}}$+$\frac{1}{3{×2}^{3}}$-$\frac{1}{4{×2}^{4}}$+…+$\frac{1}{2014{×2}^{2014}}$-$\frac{1}{2015{×2}^{2015}}$
=$\frac{1}{2}-\frac{1}{2015{×2}^{2015}}$
故答案为:$\frac{n+2}{n(n+1){•2}^{n+1}}$;$\frac{1}{n{•2}^{n}}-\frac{1}{(n+1){•2}^{n+1}}$;$\frac{1}{2}-\frac{1}{2015{×2}^{2015}}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出第n个等式的分子、分母的特征,并能用含n的代数式表示第n个等式.

练习册系列答案
相关题目
8.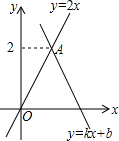 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
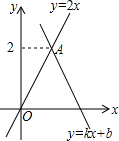 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | x>0 | B. | 0<x<1 | C. | 1<x<2 | D. | x>2 |
9.某销售公司为了提高员工的工作积极性,对员工的工资结构进行改革,改革后月工资由基本保障工资与计件奖励工资组成.(计件奖励工资=销售每件的奖励金额×销售的件数)下表是甲、乙两位职工今年三月份的工资情况信息:
求员工的月基本保障工资和销售每件产品的奖励金额各多少元?
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 100 | 80 |
| 月工资(元) | 4500 | 4100 |
13.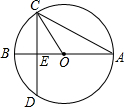 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$ | D. | 4 |
10.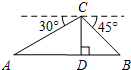 如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
 如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | 220$\sqrt{3}$米 | D. | $100(\sqrt{3}+1)$米 |
 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.