题目内容
2. 如图,观察图象,判断下列说法错误的是( )
如图,观察图象,判断下列说法错误的是( )| A. | 方程组$\left\{\begin{array}{l}y=2x-1\\ y=-\frac{3}{5}x+\frac{8}{5}\end{array}\right.$.的解是 $\left\{\begin{array}{l}x=1\\ y=1.\end{array}\right.$ | |
| B. | 不等式-$\frac{3}{5}$x+$\frac{8}{5}$≤2x-1的解集是x≥1 | |
| C. | 不等式-$\frac{3}{5}$x+$\frac{8}{5}$>2x-1的解集是x>1 | |
| D. | 方程-$\frac{3}{5}$x+$\frac{8}{5}$=2x-1的解是x=1 |
分析 根据两直线的图象即可判断不等式的解集或方程的解.
解答 解:由图象可知:两直线的交点为(1,1)
∴方程程组$\left\{\begin{array}{l}y=2x-1\\ y=-\frac{3}{5}x+\frac{8}{5}\end{array}\right.$的解是 $\left\{\begin{array}{l}x=1\\ y=1.\end{array}\right.$,
方程-$\frac{3}{5}$x+$\frac{8}{5}$=2x-1的解是x=1,故(A)与(D)正确,
当x<1时,直线y=-$\frac{3}{5}$x+$\frac{8}{5}$在y=2x-1的上方,
∴-$\frac{3}{5}$x+$\frac{8}{5}$>2x-1,
当x>1时,直线y=-$\frac{3}{5}$x+$\frac{8}{5}$在y=2x-1的下方,
∴-$\frac{3}{5}$x+$\frac{8}{5}$<2x-1,
∴x≥1时,-$\frac{3}{5}$x+$\frac{8}{5}$≤2x-1,故(B)正确,
故选(C)
点评 本题考查一次函数与不等式、方程之间的关系,解题的关键是正确理解图象所表达的信息,本题属于中等题型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
10. 如图,已知AB∥CD,∠A=70°,则∠1度数是( )
如图,已知AB∥CD,∠A=70°,则∠1度数是( )
 如图,已知AB∥CD,∠A=70°,则∠1度数是( )
如图,已知AB∥CD,∠A=70°,则∠1度数是( )| A. | 70° | B. | 110° | C. | 100° | D. | 130° |
17.当x满足( )时,$\frac{\sqrt{1+x}}{x}$在实数范围内有意义.
| A. | x>-1 | B. | x≥1且x≠0 | C. | x≥-1 | D. | x≥-1且x≠0 |
11. 如图:一张宽度相等的纸条折叠后,若∠ABC=120°,则∠1的度数是( )
如图:一张宽度相等的纸条折叠后,若∠ABC=120°,则∠1的度数是( )
 如图:一张宽度相等的纸条折叠后,若∠ABC=120°,则∠1的度数是( )
如图:一张宽度相等的纸条折叠后,若∠ABC=120°,则∠1的度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
 在数轴上表示a、b两数的点如图所示,用“>”或“<”填空:
在数轴上表示a、b两数的点如图所示,用“>”或“<”填空: 2002年国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽就是左图,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值是25.
2002年国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽就是左图,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值是25.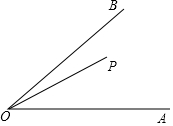 如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.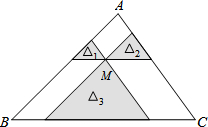 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )