题目内容
12.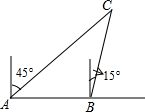 如图所示,在一条笔直的公路旁有A,B两个公交站台相距800米,居民区C位于A站台的北偏东45°方向,位于B站台的北偏东15°方向.
如图所示,在一条笔直的公路旁有A,B两个公交站台相距800米,居民区C位于A站台的北偏东45°方向,位于B站台的北偏东15°方向.(1)求居民区C到站台A的距离;(结果保留根号)
(2)为方便C居民区乘车,准备在公路旁再修建一个距C区最近的站台D,不考虑其他因素,求CD的长度.(结果保留根号)
分析 (1)作BM⊥AC,垂足为M.先解直角三角形ABM,利用已知角∠MAB的正弦值,以及AB的长,可求出AM、BM.再解直角三角形BCM中,求出CM,那么根据AC=AM+CM即可求解;
(2)过点C作CD⊥AB于点D,由△ACD是等腰直角三角形可得CD=$\frac{\sqrt{2}}{2}$AC,将(1)中所求AC的值代入计算即可.
解答 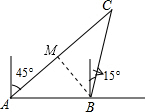 解:(1)作BM⊥AC,垂足为M.
解:(1)作BM⊥AC,垂足为M.
在直角三角形ABM中,∵∠AMB=90°,∠BAM=45°,AB=800米,
∴AM=BM=$\frac{\sqrt{2}}{2}$AB=400$\sqrt{2}$米,
在Rt△BMC中,∵∠CMB=90°,∠MBC=45°+15°=60°,
∴CM=$\sqrt{3}$BM=400$\sqrt{6}$米, ∴AC=AM+CM=(400$\sqrt{2}$+400$\sqrt{6}$)米;
∴AC=AM+CM=(400$\sqrt{2}$+400$\sqrt{6}$)米;
(2)如图,过点C作CD⊥AB于点D,
在直角三角形ACD中,
∵∠ADC=90°,∠CAD=45°,AC=(400$\sqrt{2}$+400$\sqrt{6}$)米,
∴CD=$\frac{\sqrt{2}}{2}$AC=(400+400$\sqrt{3}$)米.
点评 本题考查解直角三角形的应用-方向角问题,难度适中,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
3.正n边形的内角和不大于1000°,则n不可能是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
20.估计我国人口的百万分之一是( )
| A. | 辽宁省人数 | B. | 丹东市人数 | C. | 某中学学生数 | D. | 我班人数 |
7.下图中,主视图与俯视图不同的几何体是( )
| A. |  | B. |  | C. |  | D. |  |
2.函数y=|x|的图象是( )
| A. | 一条直线 | B. | 两条直线 | C. | 一条射线 | D. | 两条射线 |