题目内容
10. 如图,在△ABC中,CD是边AB的中线.
如图,在△ABC中,CD是边AB的中线.(1)已知CD=$\frac{1}{2}$AB,△ABC是直角三角形?请说明理由;
(2)图中还有那些线段相等,可以说明△ABC是直角三角形?写出你的结论.
分析 (1)由CD是AB边上的中线.得到AD=BD,由于CD=$\frac{1}{2}$AB,于是得到△BDC和△ADC均为等腰三角形,推出∠CBA=∠BCD,∠BAC=∠ACD,根据三角形的内角和得到∠CBA+∠BAC+∠ACD+∠BCD=180°,于是得到结论;
(2)当CD=AD=BD时,得到△BDC和△ADC均为等腰三角形,推出∠CBA=∠BCD,∠BAC=∠ACD,根据三角形的内角和得到∠CBA+∠BAC+∠ACD+∠BCD=180°,于是得到结论.
解答 解:(1)是,
理由:∵CD是AB边上的中线.
∴AD=BD,
∵CD=1/2AB,
∴CD=AD=BD,
∴△BDC和△ADC均为等腰三角形,
∴∠CBA=∠BCD,∠BAC=∠ACD,
∵∠CBA+∠BAC+∠ACD+∠BCD=180°,
∴∠BCA=∠ACD+∠BCD=180°÷2=90°,
∴△ABC是直角三角形;
(2)当CD=AD=BD时,△ABC是直角三角形.
点评 本题考查了等腰三角形和判定,直角三角形的判定,熟练掌握各定理是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
20.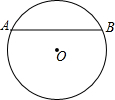 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )| A. | 24cm | B. | 13cm | C. | 14cm | D. | 15cm |
 用直尺、圆规作图:如图,Rt△ABC中,∠C=90°,在AC上找一点D,使点D到AB,BC的距离相等.
用直尺、圆规作图:如图,Rt△ABC中,∠C=90°,在AC上找一点D,使点D到AB,BC的距离相等.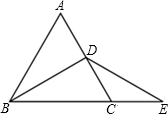 如图,在等边△ABC中,BD是高,延长BC到点E,使BC=2CE,求证:BD=DE.
如图,在等边△ABC中,BD是高,延长BC到点E,使BC=2CE,求证:BD=DE.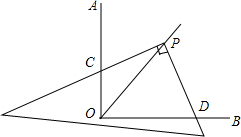 如图,∠AOB=90°,将直角三角尺的直角顶点P放在∠AOB的角平分线上,直角三角尺的两条直角边分别交OA于点C,交OB于点D,求证:PC=PD.
如图,∠AOB=90°,将直角三角尺的直角顶点P放在∠AOB的角平分线上,直角三角尺的两条直角边分别交OA于点C,交OB于点D,求证:PC=PD. 如图,在△ABC中,AF:FD=1:5,BD=DC,求AE:EC的值.
如图,在△ABC中,AF:FD=1:5,BD=DC,求AE:EC的值. 如图,试说明矩形ABCD的四个顶点在同一个圆上.
如图,试说明矩形ABCD的四个顶点在同一个圆上.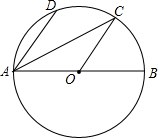 如图,AB是⊙O的直径,点D、C是⊙O上两点,且$\widehat{AD}$=$\widehat{DC}$=$\widehat{CB}$,连接AD、AC、OC,求证:OC∥AD.
如图,AB是⊙O的直径,点D、C是⊙O上两点,且$\widehat{AD}$=$\widehat{DC}$=$\widehat{CB}$,连接AD、AC、OC,求证:OC∥AD.