题目内容
16. 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线(1)求证:∠CBF=∠A;
(2)若∠A=30°,BC=2,连接OC并延长交EF于点M,求由弧BC、线段BM和CM所围成的图形的面积.
分析 (1)连结BO并延长交⊙O于H,连结HC,则∠H=∠A.由HB是直径,根据圆周角定理得出∠HCB=90°,则∠H+∠CBH=90°.再根据切线的性质得出HB⊥EF,则∠CBF+∠CBH=90°,根据同角的余角相等得出∠H=∠CBF,等量代换即可得到∠A=∠CBF;
(2)先解Rt△HCB,得出HB=4,OB=2.由∠BOM=2∠A=60°,得出BM=OB×tan60°=2$\sqrt{3}$.再根据S=S△OBM-S扇形OBC,代入数据计算即可求解.
解答 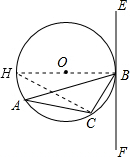 (1)证明:连结BO并延长交⊙O于H,连结HC,则∠H=∠A.
(1)证明:连结BO并延长交⊙O于H,连结HC,则∠H=∠A.
∵HB是直径,
∴∠HCB=90°,
∴∠H+∠CBH=90°.
又∵OB是半径,EF是⊙O的切线,
∴HB⊥EF,
∴∠CBF+∠CBH=90°,
∴∠H=∠CBF,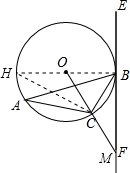 ∴∠A=∠CBF;
∴∠A=∠CBF;
(2)解:∵在Rt△HCB中,BC=2,∠H=∠A=30°,
∴HB=4,OB=2.
∵∠BOM=2∠A=60°,
∴BM=OB×tan60°=2$\sqrt{3}$.
S=S△OBM-S扇形OBC=$\frac{1}{2}OB•BM-\frac{{60π×{2^2}}}{360}$=$\frac{1}{2}×2×2\sqrt{3}-\frac{2π}{3}$=$2\sqrt{3}-\frac{2π}{3}$,
故由弧BC、线段BM和CM所围成的图形的面积为$2\sqrt{3}-\frac{2π}{3}$.
点评 本题考查了切线的性质,圆周角定理,余角的性质,扇形面积的计算,准确作出辅助线是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图所示,在高2米,宽4米的楼梯表面铺地毯,地毯的长至少需要6米.
如图所示,在高2米,宽4米的楼梯表面铺地毯,地毯的长至少需要6米.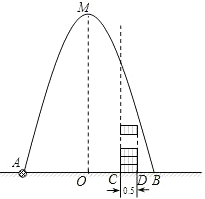 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少8个时,网球可以落入桶内.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少8个时,网球可以落入桶内.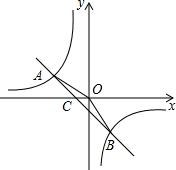 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点.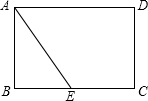 如图,有一张矩形纸片ABCD,AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.
如图,有一张矩形纸片ABCD,AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.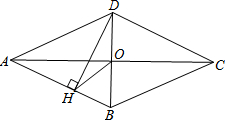 如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=25度.
如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=25度.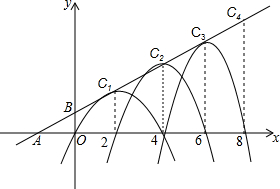 如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线ln,它们的顶点Cn(xn.yn)在直线AB上,并且经过(xn+1,0),当n=1,2,3,4…时,xn=2,4,6,8…根据上述规律,写出抛物线l7的表达式为y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.
如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线ln,它们的顶点Cn(xn.yn)在直线AB上,并且经过(xn+1,0),当n=1,2,3,4…时,xn=2,4,6,8…根据上述规律,写出抛物线l7的表达式为y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.