题目内容
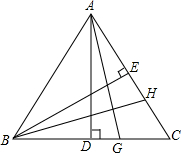如图，等边△ABC中，AD、BE是高，G、H分别是BC、AC上的点，且AG=BH．求证：CG=CH．考点：全等三角形的判定与性质,等边三角形的性质
专题：证明题
分析：易证BD=AE，AD=BE，即可证明RT△ADG≌RT△BEH，可得DG=EH，即可求得AH=BG，即可解题．
解答：证明：∵等边△ABC中，AD、BE是高，
∴AD=BE，且D，E分别是BC，AC中点，
∴BD=AE，
∵在RT△ADG和RT△BEH中，
，
∴RT△ADG≌RT△BEH，（HL）
∴DG=EH，
∴AH=BG，
∵AC=BC，
∴CG=CH．
∴AD=BE，且D，E分别是BC，AC中点，
∴BD=AE，
∵在RT△ADG和RT△BEH中，
|
∴RT△ADG≌RT△BEH，（HL）
∴DG=EH，
∴AH=BG，
∵AC=BC，
∴CG=CH．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证RT△ADG≌RT△BEH是解题的关键．
练习册系列答案
相关题目
已知△ABC与△CDE均为等边三角形，M、N为连接BE、AD时与AC、CE的交点．求证：MN∥BD．
如图，等边△ABC中，D、E分别为AB、BC边上的两动点，且总使AD=BE，AE与CD交于点F，AG⊥CD，求证：
如图，在矩形ABCD中，E、F分别是AD、BC的中点．若矩形ABCD与矩形ABFE是相似的矩形，则AD：AB=